Description
Description
The section on analytical reasoning includes the problems identifying with the including of geometrical figures a given complex figure. Determining the number of any particular type of figure by the analysis of the complex figure is in systematic method.
Reasoning Ability -BANKING|SSC|RAILWAYS|INSURANCE|RECRUITMENT EXAMS – EBOOKS
 Model
Problems
Model
Problems
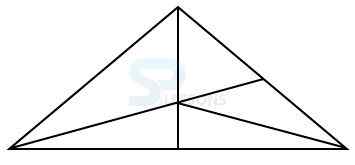
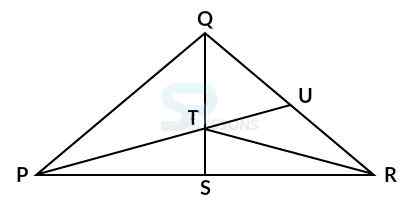
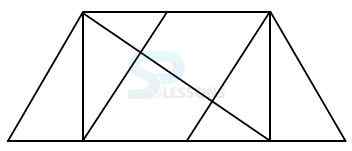
Model 1: How many triangles are there in the following figure? (R.R.B 2004)
Solution:
Let the figure is labelled as shown below:-
Simple triangles are PQT, QTU, TUR, RST and PTS i.e. 5 triangles.
The triangles composed of two components each are PQU, QRT, PTR and PQS ie. 4 triangles.
The triangles composed of three components each are PUR and QRS i.e. 2 triangles.
There is only one triangle PQR composed of five components.
Therefore, total number of triangles = 5 + 4 + 2 + 1 = 12.
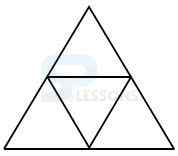
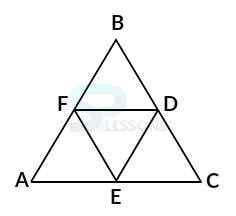
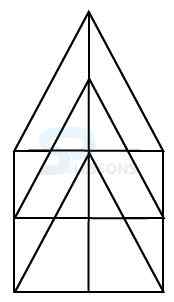
Model 2: Find the number of triangles in the given figure. (R.R.B. 2003)
Solution:
Let the figure is labelled as shown below:-
The simplest triangles are BFD, AFE, FDE and DEC i.e. 4 in number.
There is only one triangle ABC composed of four components.
Therefore, total number of triangles = 4 + 1 = 5 in the given figure.
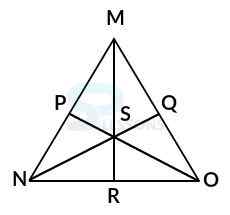
Model 3: Find the number of triangles in the given figure. (S.S.C. 2004)
Solution:
Let the figure is labelled as shown below:-
The simplest triangles are MSQ, QSO, SRO, NSR, PSN and MPS i.e. 6 in nnumber.
The triangles composed of two components each are MRO, NQO, NPO, MNR, MNQ and PMO i.e. 6 in number.
There is only one triangle i.e. MNO composed of six components.
Therefore, total number of triangles = 6 + 3 + 6 + 1 = 16 in the given figure.
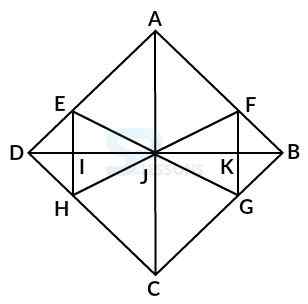
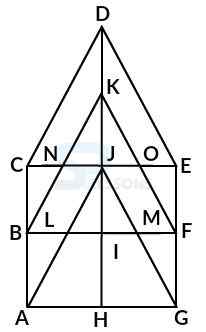
Model 4: Find the number of triangles in the given figure. (A.A.O. 2005)
Solution:
Let the figure is labelled as shown below:-
The simplest triangles are AFJ, FJK, FKB, BKG, JKG, JGC, HJC, HIJ, DIH, DEI, EIJ, and AEJ i.e. 12 in number.
The triangles composed of two components each are JFB, FBG, BJG, JFG, DEJ, EJH, DJH and DEH i.e. 8 in number.
The triangles composed of three components each are AJB, JBC, DJC and ADJ i.e. 4 in number.
The triangles composed of six components each are DAB, ABC, BCD, and ADC i.e. 4 in number.
Therefore, total number of triangles = 12 + 8 + 4 + 4 = 28 triangles in the figure.
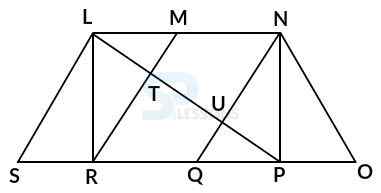
Model 5: Find the number of triangles in the given figure. (M.B.A. 2005)
Solution:
Let the figure is labelled as shown below:-
The simplest triangles are LSR, LTR, LTM, UQP, NUP, and NPO i.e. 6 in number.
The triangles composed of two components each are LMR, NQP, LNU and PRT i.e. 4 in number.
The triangles composed of three components each are LNP, LRP and NQO i.e. 3 in number.
There is only one triangle i.e. LSP of four components.
Therefore, total number of triangles = 6 + 4 + 3 + 1 = 14 from the given figure.
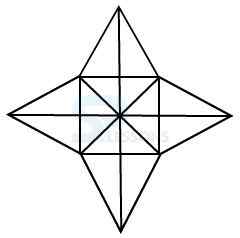
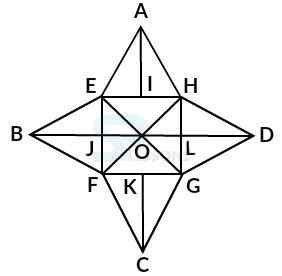
Model 6: Find the number of triangles in the given figure. (S.S.C. 2004)
Solution:
Let the figure is labelled as shown below:-
The simplest triangles are AEI, AIH, BEJ, BJF, CFK, CKG, DGL, DLH, EOJ, FOJ, LOG, HOL and HOE i.e. 14 in number.
The triangles composed of two components each are EAH, FBE, BEO, EOF, BFO, FCG, GDH, HOD, HOG and GOD i.e. 10 in number.
The triangles composed of three components each are EFH, EHG, FGH and EFG i.e. 4 in number.
Therefore, there are 14 + 10 + 4 = 28 triangles in the given figure.
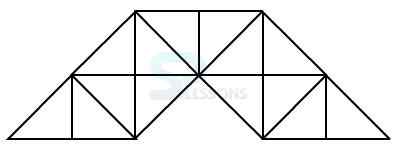
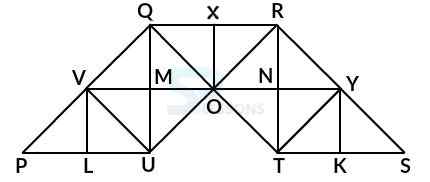
Model 7: Find the number of triangles in the given figure. (L.I.C. A.A.O. 2005)
Solution:
Let the figure is labelled as shown below:-
The simplest triangles are PVL, LVU, UVM, VMQ, UMO, VMQ, UMO, QMO, QXO, RXO, ONR, RNY, ONT, NTY, TKY and YKS i.e. 14 in number.
The triangles composed of two components each are PUV, QUV, VQO, QOU, VOU, QRO, RYO, RYT, YTO, ROT and YTS i.e. 11 in number.
The triangles composed of four components each are PQU, RQU, QRT and RTS i.e. 4 in number.
Therefore, total number of triangles in the given figure = 14 + 11 + 4 = 29.
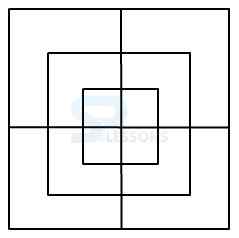
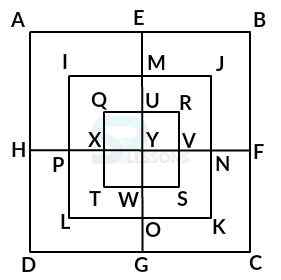
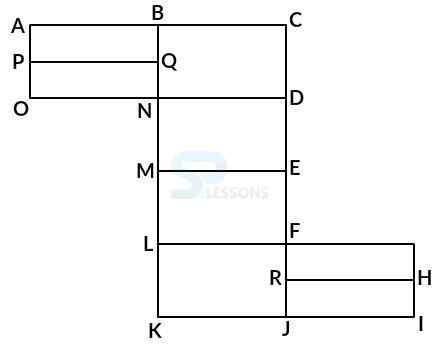
Model 8: Count the number of squares in the given figure. (Railways 2006)
Solution:
Let the figure is labelled as shown below:-
The simplest squares are QUYX, URVY, YVSW and XYWT i.e. 4 in number.
The squares composed of two components each are IMYP, MJNY, YNKO and PYOL i.e. 4 in number.
The squares composed of three components each are AEYH, EBFY, YFCG, and HYGD i.e. 4 in number.
There is only one square i.e. QRST composed of four components.
There is only one square i.e. IJKL composed of eight components.
There is only one square i.e. ABCD composed of twelve components.
Therefore, total number of squares in the given figure = 4 + 4 + 4 + 1 + 1 + 1 = 15.
Model 9: How many triangles and parallelograms are there in the following figure? (M.B.A. 2006)
Solution:
Let the figure is labelled as shown below:-
Triangles:-
The simplest triangles are KJN, KJO, CNB, OEF, JIL, JIM, BLA and MFG i.e. 8 in number.
The triangles composed of two components each are CDJ, EDJ, NKO, JLM, JAH and JGH i.e. 6 in number.
The triangles composed of three components each are BKI, FKI, CJA, EJG i.e. 4 in number.
The triangles composed of four components each are CDE and AJG i.e. 4 in number.
The only triangle composed of six components is BKF.
Therefore, there are 8 + 6 + 4 + 2 + 1 = 21 triangles in the given figure.
Parallelogram:-
Here, squares and rectangles can also be considered as parallelograms.
The simplest parallelograms are NJLB and JOFM i.e. 2 in number.
The parallelograms composed of two components each are CDKB, DEFK, BIHA and IFGH i.e. 4 in number.
The parallelograms composed of three components each are BKJA, KFGJ, CJIB and JEFI i.e. 4 in n umber
There is only one parallelogram i.e. BFGA composed composed of four components.
The parallelograms composed of five components each are CDJA, DEGJ, CJHA and JEGH i.e. 4 in number.
There is only one parallelogram i.e. CEFB composed composed of six components.
There is only one parallelogram i.e. CEGA composed composed of ten components.
Therefore, there are 2 + 4 + 4 + 1 + 4 + 1 + 1 = 17 parallelograms in the given figure.
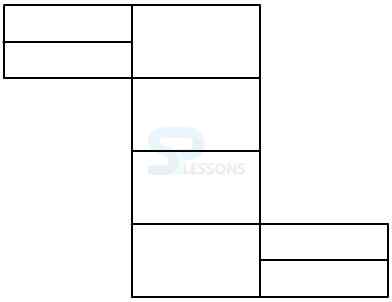
Model 10: Count the number of rectangles in the given figure. (N.M.A.T. 2005)
Solution:
Let the figure is labelled as shown below:-
The simplest rectangles are ABQP, PQNO, BCDN, NDEM, MEFL, LFJK, FGHR, and RHIJ i.e. 8 in number.
The rectangles composed of two components each are ABNO, BCEM, NDFL, MEJK and FGIJ i.e. 5 in number.
The rectangles composed of three components each are ACDO, BCFL, NDJK and LGIK i.e. 4 in number.
There is only one rectangle i.e. BCJK composed of four components.
Therefore, total number of rectangles in the figure = 8 + 5 + 4 + 1 = 18.