Introduction
Introduction
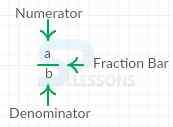
A fraction is a number of the form [latex]\frac{a}{b}[/latex], where ‘a’ and ‘b’ are integers and b is not equal to zero since division by zero is undefined.
In essence, one can think a fraction as another way of writing a division problem.
Example: [latex]\frac{4}{5}[/latex] is also written as 4 ÷ 5.
Quantitative Aptitude -BANKING|SSC|RAILWAYS|INSURANCE|RECRUITMENT EXAMS - EBOOKS
 Methods
Methods
In general, the integer on the top of the fraction bar is called the numerator and the integer underneath the fraction bar is called the denominator.
Example: [latex]\frac{-5}{3}[/latex]
Negative 5 over 3 is a fraction in which -5 is numerator and 3 is the denominator.
These types of numbers are also referred to as rational numbers.
Properties:
1. If both the numerator ‘a’ and ‘b’ are multiplied by the same non-zero integer, the resulting fraction will be equivalent to a/b.
Example:
- [latex]\frac{-5}{3}[/latex]
[latex]\frac{-5}{3}[/latex] = [latex]\frac{(-5)}{3}[/latex] * [latex]\frac{4}{4}[/latex] = [latex]\frac{-20}{12}[/latex]
Here, [latex]\frac{-20}{12}[/latex] is equivalent to [latex]\frac{-5}{3}[/latex]
[latex]\frac{-5}{3}[/latex] = [latex]\frac{(-5)}{3}[/latex] * [latex]\frac{(-1)}{(-1)}[/latex] = [latex]\frac{5}{-3}[/latex]
- [latex]\frac{40}{72}[/latex]
Numerator can be written as 8 * 5
Denominator can be written as 8 * 9
[latex]\frac{40}{72}[/latex] = [latex]\frac{(8 * 5)}{(8 * 9)}[/latex] = [latex]\frac{5}{9}[/latex]
- By prime factorization
[latex]\frac{16}{20}[/latex] = [latex]\frac{(2 * 2 * 2 * 2)}{(2 * 2 * 5)}[/latex] = [latex]\frac{4}{5}[/latex]
- By Greatest Common factor (GCF)
[latex]\frac{16}{20}[/latex] = [latex]\frac{(\frac{16}{4})}{(\frac{20}{4})}[/latex] = [latex]\frac{4}{5}[/latex]
Note:
Before solving any fractions first always reduce the fractions.
3. A fraction with a negative sign in either the numerator or denominator can be written with the negative sign in front of the fraction.
Example 1:
- [latex]\frac{-5}{3}[/latex] = [latex]\frac{5}{-3}[/latex] = -[latex]\frac{5}{-3}[/latex]
- [latex]\frac{-5}{-3}[/latex] = [latex]\frac{5}{3}[/latex] (Since - x - = +)
- [latex]\frac{1}{10}[/latex] + [latex]\frac{2}{10}[/latex] = [latex]\frac{(1 + 2)}{10}[/latex] = [latex]\frac{3}{10}[/latex]
- [latex]\frac{5}{11}[/latex] – [latex]\frac{8}{11}[/latex] = [latex]\frac{(5 - 8)}{11}[/latex] = [latex]\frac{-3}{11}[/latex]
- [latex]\frac{1}{5}[/latex] + [latex]\frac{2}{5}[/latex] + [latex]\frac{3}{5}[/latex] = [latex]\frac{(1 + 2 + 3)}{5}[/latex] = [latex]\frac{6}{5}[/latex]
- [latex]\frac{2}{3}[/latex] + [latex]\frac{3}{4}[/latex]
LCM of 3 and 4 is 12.
[latex]\frac{((4 * 2) + (3 * 3))}{12}[/latex]
[latex]\frac{(8 + 9)}{12}[/latex]
[latex]\frac{17}{12}[/latex]
- [latex]\frac{1}{3}[/latex] – [latex]\frac{2}{5}[/latex]
LCM of 3 and 5 is 15.
[latex]\frac{((1 * 5) – (2 * 3))}{15}[/latex]
[latex]\frac{(5 - 6)}{15}[/latex]
= -[latex]\frac{1}{15}[/latex]
- [latex]\frac{2}{3}[/latex] + [latex]\frac{1}{5}[/latex] – [latex]\frac{1}{2}[/latex]
LCM of 3, 5, 2 is 30
[latex]\frac{((2 * 10) + (1 * 6) - (15 *1))}{30}[/latex]
[latex]\frac{(20 + 6 – 15)}{30}[/latex]
[latex]\frac{11}{30}[/latex]
- [latex]\frac{8}{3}[/latex] * [latex]\frac{7}{3}[/latex] = [latex]\frac{(8 * 7)}{(3 * 3)}[/latex] = [latex]\frac{56}{9}[/latex]
Note:
Always simplify fractions whenever possible.
Example 2:
- [latex]\frac{4}{5}[/latex] * [latex]\frac{10}{12}[/latex] = [latex]\frac{(4 * 10)}{(5 * 12)}[/latex] = [latex]\frac{40}{60}[/latex] = [latex]\frac{4}{6}[/latex] = [latex]\frac{2}{3}[/latex]
Note: Do not try to simplify fractions while adding or subtracting the terms.
Need to find the common denominator, before adding or subtracting fractions.
When an integer is multiplied to a fraction
Example 1:
- 2 * [latex]\frac{4}{5}[/latex] = [latex]\frac{2}{1}[/latex] * [latex]\frac{4}{5}[/latex] = [latex]\frac{8}{5}[/latex]
- [latex]\frac{3}{36}[/latex] * 3 = [latex]\frac{3}{36}[/latex] * [latex]\frac{3}{1}[/latex] = [latex]\frac{9}{36}[/latex] = [latex]\frac{1}{4}[/latex]
- [latex]\frac{17}{8}[/latex] ÷ [latex]\frac{3}{4}[/latex] = [latex]\frac{17}{8}[/latex] * [latex]\frac{4}{3}[/latex] = [latex]\frac{(17 * 4)}{(8 * 3)}[/latex] = [latex]\frac{17}{6}[/latex]
- [latex]\frac{4}{3}[/latex] ÷ 3 = [latex]\frac{4}{3}[/latex] ÷ 3 = [latex]\frac{4}{3}[/latex] * [latex]\frac{1}{3}[/latex] = [latex]\frac{4}{9}[/latex]
- [latex]\frac{7}{\frac{1}{4}}[/latex] = [latex]\frac{7}{1}[/latex] ÷ [latex]\frac{1}{4}[/latex] = [latex]\frac{7}{1}[/latex] * [latex]\frac{4}{1}[/latex] = 28
- [latex]\frac{\frac{3}{10}}{\frac{7}{13}}[/latex] = [latex]\frac{3}{10}[/latex] ÷ [latex]\frac{7}{13}[/latex] = [latex]\frac{3}{10}[/latex] * [latex]\frac{13}{7}[/latex] = [latex]\frac{39}{70}[/latex]
- [latex]4\frac{3}{8}[/latex]
[latex]4\frac{3}{8}[/latex] = 4 + [latex]\frac{3}{8}[/latex] = [latex]\frac{4}{1}[/latex] + [latex]\frac{3}{8}[/latex]
LCM of 1 and 8 is 8
[latex]\frac{(32 + 3)}{8}[/latex] = [latex]\frac{35}{8}[/latex]
Here, 35/8 is a improper fraction.
- Compare [latex]\frac{3}{7}[/latex] and [latex]\frac{7}{12}[/latex]
[latex]\frac{3}{7}[/latex] and [latex]\frac{7}{12}[/latex]
[latex]\frac{(12)(3)}{(12)(7)}[/latex] and [latex]\frac{(7)(7)}{(12)(7)}[/latex]
[latex]\frac{36}{84}[/latex] and [latex]\frac{49}{84}[/latex]
As the denominators are same, now compare the numerators
Like [latex]\frac{49}{84}[/latex] is bigger
[latex]\frac{36}{84}[/latex] is smaller
[latex]\frac{36}{84}[/latex] < [latex]\frac{49}{84}[/latex]
- [latex]\frac{π}{2}[/latex] + [latex]\frac{π}{3}[/latex] = [latex]\frac{(3π +2π)}{6}[/latex] = [latex]\frac{5π}{6}[/latex]
- [latex]\frac{π}{2}[/latex] * [latex]\frac{π}{3}[/latex] = [latex]\frac{π^2}{6}[/latex]
- [latex]\frac{(\frac{π}{2})}{(\frac{π}{3})}[/latex] = [latex]\frac{π}{2}[/latex] * [latex]\frac{3}{π}[/latex] = [latex]\frac{3π}{2π}[/latex] = [latex]\frac{3}{2}[/latex]
 Samples
Samples
1. Quantitative Comparison
| Column A | Column B |
|---|---|
| 5 | y |
- A. Column A is greater.
B. Column B is greater.
C. The two quantities are equal.
D. The relationship cannot be determined from the information given.
- [latex]\frac{x}{y}[/latex] = [latex]\frac{1}{5}[/latex]
By cross multiplication,
5x = y
It is given that x is a positive integer. That could mean x is 1, 2, 3, ....
If x is 1, then y would equal 5. However, if x is an integer greater than or equal to 2 then y would be greater than 5. Since we don’t know x’s exact value, then we cannot determine the relationship between 5 and y.
Hence, option D is the right choice.
- A. 14
B. [latex]\frac{26}{3}[/latex]
C. [latex]\frac{28}{2}[/latex]
D. [latex]\frac{28}{3}[/latex]
- To simplify the given fraction, simply invert the denominator and multiply by the numerator:
[latex]\frac{ \frac{2}{3}}{\frac{1}{5}}[/latex] + [latex]\frac{9}{\frac{3}{2}} [/latex]
Multiply the denominator by the reciprocal of the denominator for each term:
[latex]\frac{2}{3}[/latex] * [latex]\frac{5}{1}[/latex] + [latex]\frac{9}{1}[/latex] * [latex]\frac{2}{3}[/latex]
= [latex]\frac{10}{3}[/latex] + [latex]\frac{18}{3}[/latex]
Since the denominator is same, add both the terms:
= [latex]\frac{28}{3}[/latex]
Hence, option D is the right choice.
- A. [latex]\frac{7}{8}[/latex]
B. [latex]\frac{1}{3}[/latex]
C. [latex]\frac{2}{3}[/latex]
D. [latex]\frac{1}{2}[/latex]
- [latex]\frac{3}{5}[/latex] = 0.6
[latex]\frac{6}{7}[/latex] = 0.85 (Taken only the first two digits after the decimal point)
Hence, the question is to find out a number which is greater than 0.6 and less than 0.85
The given choices are
[latex]\frac{1}{2}[/latex] = 0.5
[latex]\frac{2}{3}[/latex] = 0.66 (Taken only the first two digits after the decimal point)
[latex]\frac{1}{3}[/latex] = 0.33 (Taken only the first two digits after the decimal point)
[latex]\frac{7}{8}[/latex] = 0.87 (Taken only the first two digits after the decimal point)
Clearly, 0.66 = [latex]\frac{2}{3}[/latex] is the answer.
- A. [latex]\frac{7}{8}[/latex], [latex]\frac{4}{7}[/latex], [latex]\frac{3}{7}[/latex], [latex]\frac{2}{5}[/latex], [latex]\frac{1}{4}[/latex], [latex]\frac{1}{6}[/latex]
B. None of these
C. [latex]\frac{1}{4}[/latex], [latex]\frac{2}{5}[/latex], [latex]\frac{4}{7}[/latex], [latex]\frac{1}{6}[/latex], [latex]\frac{3}{7}[/latex], [latex]\frac{7}{8}[/latex]
D. [latex]\frac{1}{4}[/latex], [latex]\frac{2}{5}[/latex], [latex]\frac{4}{7}[/latex], [latex]\frac{5}{6}[/latex], [latex]\frac{6}{7}[/latex], [latex]\frac{7}{8}[/latex]
- [latex]\frac{1}{4}[/latex] = 0.25 and [latex]\frac{2}{5}[/latex] = 0.4
Hence, [latex]\frac{2}{5}[/latex] > 1/4
Hence, [latex]\frac{1}{4}[/latex], [latex]\frac{2}{5}[/latex], [latex]\frac{4}{7}[/latex], [latex]\frac{5}{6}[/latex], [latex]\frac{6}{7}[/latex], [latex]\frac{7}{8}[/latex] is not in descending order.
Similarly, [latex]\frac{1}{4}[/latex], [latex]\frac{2}{5}[/latex], [latex]\frac{4}{7}[/latex], [latex]\frac{1}{6}[/latex], [latex]\frac{3}{7}[/latex], [latex]\frac{7}{8}[/latex] is also not in descending order.
[latex]\frac{7}{8}[/latex] = 0.8 (Taken only one digit after the decimal point)
[latex]\frac{4}{7}[/latex] = 0.5 (Taken only one digit after the decimal point)
[latex]\frac{3}{7}[/latex] = 0.42 (Taken only two digits after the decimal point)
[latex]\frac{2}{5}[/latex] = 0.4
[latex]\frac{1}{4}[/latex] = 0.2 (Taken only one digit after the decimal point)
[latex]\frac{1}{6}[/latex] = 0.1 (Taken only one digit after the decimal point)
Hence,
[latex]\frac{7}{8}[/latex], [latex]\frac{4}{7}[/latex], [latex]\frac{3}{7}[/latex], [latex]\frac{2}{5}[/latex], [latex]\frac{1}{4}[/latex], [latex]\frac{1}{6}[/latex] is in descending order.
- A. [latex]\frac{1}{5}[/latex]
B. [latex]\frac{2}{9}[/latex]
C. [latex]\frac{23}{99}[/latex]
D. [latex]\frac{23}{100}[/latex]
- 0.232323... = [latex]\bar{23}[/latex] = [latex]\frac{23}{99}[/latex]