Introduction
Introduction
What is Quantitative Aptitude test?
Quantitative Aptitude is one of the prominent competitive aptitude subjects which evaluates numerical ability and problem solving skills of candidates. This test forms the major part of a number of important entrance and recruitment exams for different fields. The Quantitative Aptitude section primarily has questions related to the Simplification, Numbering Series, and Compound Interest, etc.
A candidate with quantitative aptitude knowledge will be in a better position to analyse and make sense of the given data. Quantitative Aptitude knowledge is an important measure for a prospective business executive's abilities.
The article IBPS Clerk Numerical Ability Quiz 4 provides Quantitative Aptitude questions with answers useful to the candidates preparing for Competitive exams, Entrance exams, Interviews etc.
 Quiz
Quiz
Direction[1-3]: What should come in place of the question mark (?) in the following number series?
1. 30 , 62 , 189 , ? , 3805 , 22836
- A. 860
B. 760
C. 560
D. 555
E. 654
- A. 420
B. 99
C. 126
D. 386
E. 102
- A. 70
B. 45
C. 30
D. 72
E. 61
- A. 28
B. 33
C. 46
D. 56
E. 37
- A. 208 km
B. 283 km
C. 324 km
D. 378 km
E. None of these
1. Six spherical cannon balls are tightly packed into a rectangular box in one layer. Each row has two cannon balls and each column has three. What part of the box is empty?
- A. 11
B. [latex]\frac {10}{21}[/latex]
C. [latex]\frac {15}{21}[/latex]
D. 5
E. 20
- A. 3 : 5
B. 4 : 5
C. 3 : 2
D. 2 : 3
E. None of these
- A. 1150
B. 1050
C. 1156
D. 1256
E. 1080
- A. 88
B. 16
C. 113
D. 329
E. 444
- A. 165
B. 85
C. 110
D. 200
E. 135
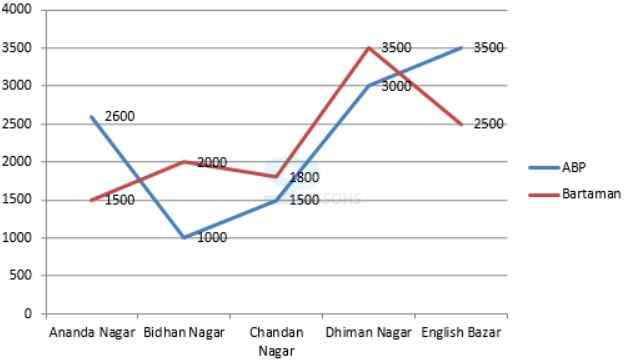
Direction[1-5]: Read the line chart given below and answer the question that follow.
1. What is the difference between the total sale of Bartaman newspaper and the total sale of ABP newspaper in all the localities together?
- A. 400
B. 360
C. 350
D. 300
E. None of the above
- A. 18%
B. 20%
C. 22%
D. 15%
E. 12%
- A. 13 : 12
B. 4 : 3
C. 5 : 4
D. 7 : 3
E. None of these
- A. 72.33%
B. 68.33%
C. 50%
D. 58%
E. 60%
- A. 4750
B. 4850
C. 5000
D. 2890
E. None of these