1. The area of a sector of a circle of radius 36 cm is 72π[latex]{cm}^{2}[/latex]. The length of the corresponding arc of the sector is

A. π cm B. 2π cm C. 3π cm D. 4π cm

Answer: Option: D
Explanation: Given that, radius (r) = 36 cm And, Area of sector = 72π [latex]{cm}^{2}[/latex] ⇒ πr2θ = [latex]\frac{72π}{360°}[/latex] ∴ θ = [latex]\frac{72π × 360°}{π{r}^{2}}[/latex] = 72 × 360° =[latex]\frac{20°}{36 × 36}[/latex] Now, length of arc = [latex]\frac{πrΘ}{180°}[/latex] = π × 36 × 20° = 4π cm
2. A square is inscribed in a circle of diameter 2a and another square is circumscribing circle. The difference between the areas of outer and inner squares is

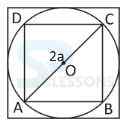
A. [latex]{a}^{2}[/latex] B. 2[latex]{a}^{2}[/latex] C. 3[latex]{a}^{2}[/latex] D. 4[latex]{a}^{2}[/latex]

Answer: Option: B
Explanation: Given that, Diameter = 2a For inscribed square, Diameter of circle = Diagonal of inner square For circumscribed square, Diameter of circle = Side of outer square ∴ Area of inner square = [latex]\frac{1}{2}[/latex] [latex]{(diagonal)}^{2}[/latex] = [latex]\frac{1}{2}[/latex] × [latex]{(2a)}^{2}[/latex] = 2[latex]{a}^{2}[/latex] And, Area of outer square = [latex]{(side)}^{2}[/latex] = [latex]{(2a)}^{2}[/latex] = 4[latex]{a}^{2}[/latex] Now, Required difference = 4[latex]{a}^{2}[/latex] – 2[latex]{a}^{2}[/latex] = 2[latex]{a}^{2}[/latex]
3. ABC is a triangle right angled at A. AB = 6 cm and AC = 8 cm. Semi-circles drawn (outside the triangle) on AB, AC and BC as diameters which enclose areas x, y and z square units, respectively. What is x + y – z equal to ?

A. 48 [latex]{cm}^{2}[/latex] B. 32 [latex]{cm}^{2}[/latex] C. 0 D. None of these

Answer: Option: C
Explanation: Given that, AB = 6 cm and AC = 8 cm In ΔABC, by Pythagoras theorem, BC = [latex]{AB}^{2}[/latex] +[latex]{AC}^{2}[/latex] = 62 + 82 = 100 = 10 cm Now, Area of that semi-circle which diameter is AB = [latex]\frac{{π(3)}^{2}}{2}[/latex] ∴ x = 9π [latex]{cm}^{2}[/latex] 2 Similarly, Area of that semi-circle which diameter is AC = [latex]\frac{{π(4)}^{2}}{2}[/latex] ∴ y = 16π [latex]{cm}^{2}[/latex] 2 Similarly, Area of that semi-circle which diameter is BC = [latex]\frac{{π(5)}^{2}}{2}[/latex] ∴ z = [latex]\frac{25π}{2}[/latex] [latex]{cm}^{2}[/latex] Now, x + y – z = ([latex]\frac{9π}{2}[/latex] + [latex]\frac{16π}{2}[/latex]) – [latex]\frac{25π}{2}[/latex] = 0
4. Consider an equiateral triangle of a side of unit length. A new equilateral triangle is formed by joining the mid-points of one, then a third equilateral triangle is formed by joining the mid-points of second. The process is continued. The perimeter of all triangles, thus formed is

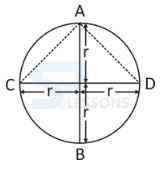
A. 2 units B. 3 units C. 6 units D. infinity

Answer: Option: C
Explanation: Perimeter of all triangles = (3 × 1) + (3 × 0.5) + (3 × 0.25) + (3 × 0.125) = 3 + 1.5 + 0.75 + 0.375 = 5.625 ≈ 6 units
5. If AB and CD are two diameters of a circle of radius r and they are mutually perpendicular, then what is the ratio of the area of the circle to the area of the ΔACD ?

A. [latex]\frac{π}{2}[/latex] B. π C.[latex]\frac{π}{4}[/latex] D. 2π

Answer: Option: B
Explanation: Required ratio = Area of circle : Area of ΔACD = π[latex]\frac{{r}^{2}}{ 1 × 2r × r}[/latex] = [latex]\frac{π}{2}[/latex]

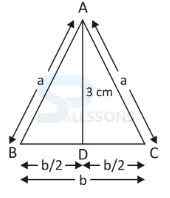
1. The area of an isosceles ΔABC with AB = AC and altitude AD = 3 cm is 12 sq cm. What is its perimeter ?

A. 18 cm B. 16 cm C. 14 cm D. 12 cm

Answer: Option: A
Explanation: Given, Area of triangle ABC = 12 [latex]{cm}^{2}[/latex] ∴ [latex]\frac{1}{2}[/latex] × h × b = 12 ⇒ [latex]\frac{1}{2}[/latex] × 3 × b = 12 ⇒ b = 8 cm Here, BD = CD = [latex]\frac{b}{2}[/latex] = [latex]\frac{8}{2}[/latex] = 4 cm In right-angled ΔABD, by pythagoras theorem, AB = [latex]{AD}^{2}[/latex] + [latex]{BD}^{2}[/latex] a = [latex]{3}^{2}[/latex] + [latex]{4}^{2}[/latex] = 25 = 5 cm Now, perimeter of an isosceles triangle = 2a + b = 2 × 5 + 8 = 18 cm
2. What is the area between a square of side 10 cm and two inverted semi-circular, cross-sections each of radius 5 cm inscribed in the square ?

A. 17.5 [latex]{cm}^{2}[/latex] B. 18.5 [latex]{cm}^{2}[/latex] C. 20.5 [latex]{cm}^{2}[/latex] D. 21.5 [latex]{cm}^{2}[/latex]

Answer: Option: D
Explanation: Given, each side of a square (a) = 10 cm and, radius of each semi-circular (r) = 5 cm Area between square and semi-circules = Area of square – 2 Area of semi-circle = [latex]{a}^{2}[/latex] – 2 × [latex]\frac{1}{3}[/latex] π[latex]{r}^{2}[/latex] = (10)2 – 2 × [latex]\frac{1}{2}[/latex] × [latex]\frac{22}{7}[/latex] × [latex]{(5)}^{2}[/latex] = 100 – 78.5 = 21.5 [latex]{cm}^{2}[/latex]
3. The perimeter of a rectangle having area equal to 144 cm2 and sides in the ratio 4 : 9 is

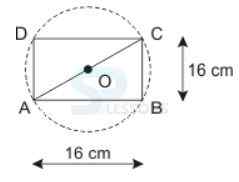
A. 52 [latex]{cm}^{2}[/latex] B. 56 [latex]{cm}^{2}[/latex] C. 60 [latex]{cm}^{2}[/latex] D. 64 [latex]{cm}^{2}[/latex]

Answer: Option: A
Explanation: Let, length of rectangle (l) = 4x and breadth of rectangle (b) = 9x ∴ Area of rectangle = l × b ⇒ 144 = 4x × 9x = 36[latex]{x}^{2}[/latex] ⇒ [latex]{x}^{2}[/latex] = 4 ⇒ x = 2 Now, l = 4x = 4 × 2 = 8 cm and b = 9x = 9 × 2 = 18 cm ∴ Perimeter of rectangle = 2(l + b) = 2 (8 + 18) = 52 [latex]{cm}^{2}[/latex]
4. One side of a parallelogram is 8.06 cm and its perpendicular distance from opposite side is 2.08 cm. What is the approximate area of the parallelogram ?

A. 12.56 [latex]{cm}^{2}[/latex] B. 14.56 [latex]{cm}^{2}[/latex] C. 16.76 [latex]{cm}^{2}[/latex] D. 22.56 [latex]{cm}^{2}[/latex]

Answer: Option: C
Explanation: Area of parallelogram = Base × Height = 8.06 × 2.08 = 16.76 [latex]{cm}^{2}[/latex]
5. In the figure given below, the area of rectangle ABCD is 100 sq cm, O is any point on AB and CD = 20 cm. Then, the area of ΔCOD is

A. 40 [latex]{cm}^{2}[/latex] B. 45 [latex]{cm}^{2}[/latex] C. 50 [latex]{cm}^{2}[/latex] D. 80 [latex]{cm}^{2}[/latex]

Answer: Option: C
Explanation: Given that, CD = 20 cm And, area of rectangle ABCD = 100 [latex]{cm}^{2}[/latex] ⇒ AD × CD = 100 ⇒ AD × 20 = 100 ⇒ AD = 5 cm ∵ AD = OP = 5 cm ∴ Area of ΔCOD = [latex]\frac{1}{2}[/latex] × CD × OP = [latex]\frac{1}{2}[/latex] × 20 × 5 = 50 [latex]{cm}^{2}[/latex]

1. A piece of wire 78 cm long is bent in the form of an isosceles triangle. If the 1. ratio of one of the equal sides to the base is 5 : 3, then what is the length of the base?

A. 16 cm B. 18 cm C. 20 cm D. 30 cm

Answer: Option: B
Explanation: Let the sides of isosceles triangle is 5x, 5x and 3x cm respectively. By given condition, Perimeter of isosceles triangle = Length of wire ⇒ 5x + 5x + 3x = 78 ⇒ 13x = 78 ⇒ x = 6 cm ∴ Length of base = 3x = 3 × 6 = 18 cm
2. The length of a minute hand of a wall clock is 9 cm. What is the area swept (in cm2) by the minute hand in 20 min ? (take π = 3.14)

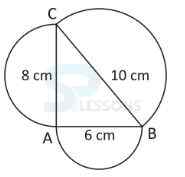
A. 88.78 B. 84.78 C. 67.74 D. 57.78

Answer: Option: B
Explanation: Given, r = 9 cm The angle made by the minute hand in 20 min, θ = 120° ∴ The area swept by the minute hand in 20 min = θ × [latex]\frac{π{r}^{2}}{360°}[/latex] = [latex]\frac{120° × 3.14 × 9 × 9}{360°}[/latex] = 84.78 [latex]{cm}^{2}[/latex]
3. If the area of a ΔABC is equal to area of square of sde length 6 cm, then what is the length of the altitude to AB, where AB = 9 cm ?

A. 18 cm B. 14 cm C. 12 cm D. 8 cm

Answer: Option: D
Explanation: Given, AB = 9 cm Let the length of altitude to AB = l cm By given condition, Area of ΔABC = Area of square ∴ [latex]\frac{1}{2}[/latex] × Base × Altitude = [latex]{(Side length)}^{2}[/latex] ⇒ [latex]\frac{1}{2}[/latex] × 9 × l = 36 ⇒ l = [latex]\frac{36 × 2}{9}[/latex] = 8 cm
4. What is the area of an equilateral triangle having altitude equal to 2√3 cm?

A. √3 sq cm B. 2√3 sq cm C. 3√3 sq cm D. 4√3 sq cm

Answer: Option: D
Explanation: We know that, altitude of an equilateral triangle = [latex]\frac{√3}{2}[/latex] a ⇒ 2√3 = [latex]\frac{√3}{2}[/latex] a ⇒ a = 4 cm ∴ Area of equilateral triangle = [latex]\frac{√3}{4}[/latex] [latex]{a}^{2}[/latex] = [latex]\frac{√3}{4}[/latex] × [latex]{(4)}^{2}[/latex] = 4√3 [latex]{cm}^{2}[/latex]
5. If a circle circumscribes a rectangle with side 16 cm and 12 cm, then what is the area of the circle ?

A. 48π sq cm B. 50π sq cm C. 100π sq cm D. 200π sq cm

Answer: Option: C
Explanation: In right-angled ΔABC, AC = [latex]\sqrt{{AB}^{2} + {BC}^{2}}[/latex] = [latex]\sqrt{{16}^{2} + {12}^{2}}[/latex] = [latex]\sqrt{400}[/latex] = 20 cm Diameter of circumcircle = 20 cm ∴ Radius of circumcircle (r) = 10 cm Area of circumcircle = π[latex]{r}^{2}[/latex] = π × [latex]{(10)}^{2}[/latex] = 100π [latex]{cm}^{2}[/latex]