Introduction
Introduction
What is Quantitative Aptitude test?
Quantitative Aptitude is one of the prominent competitive aptitude subjects which evaluates numerical ability and problem solving skills of candidates. This test forms the major part of a number of important entrance and recruitment exams for different fields. The Quantitative Aptitude section primarily has questions related to the Simplification, Numbering Series, and Compound Interest, etc.
A candidate with quantitative aptitude knowledge will be in a better position to analyse and make sense of the given data. Quantitative Aptitude knowledge is an important measure for a prospective business executive's abilities.
The article IBPS RRB Quantitative Aptitude Quiz Day 6 provides Quantitative Aptitude questions with answers useful to the candidates preparing for Competitive exams, Entrance exams, Interviews etc. IBPS RRB has released IBPS RRB Officer 2019 Official Notification for Officer Scale(I, II, and II). Quantitative Aptitude plays major role to qualify examination. The article IBPS RRB Quantitative Aptitude Quiz Day 6 will assist the students to know the expected questions from Quantitative Aptitude.
Click Here for Official IBPS Website
 Quiz
Quiz
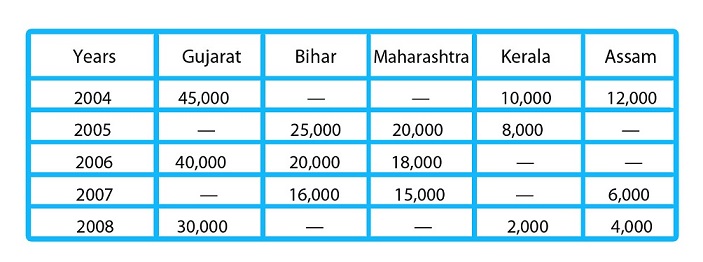
Directions (1-5): The following table shows the number of persons who got injured in earthquake from five different states of India during five different years. Study the table carefully to answer the following questions.
Q1. If total no. of person in Maharashtra who injured due to earthquake in 2004 was 150% more than the total no. of person from same state who injured in earthquake in 2008, then the total no. of person who injured in earthquake in 2005 in Maharashtra is what percent of total no. of persons who injured in 2008 in same state (It is given that total persons who injured in earthquake in Maharashtra throughout all the years is 88,000)?
-
A. 190%
B. 210%
C. 200%
D. 150%
E. 250%
-
A. 25% more
B. 25% less
C. 20% less
D. 20% more
E. 30% less
-
A. 1,05,000
B. 1,50,000
C. 1,10,000
D. 95,000
E. 1,15,000
-
A. 54,160
B. 55,160
C. 58,160
D. 57,160
E. 49,260
-
A. [latex] \frac{400} {7}[/latex]%
B. [latex] \frac{300} {7}[/latex]%
C. [latex] \frac{200} {7}[/latex]%
D. [latex] \frac{100} {7}[/latex]%
E. [latex] \frac{500} {7}[/latex]%
Directions (1-5): The table given below provides the percentage of number of students from 5 different colleges who got placed in various companies during campus placement in year 2016. It was recorded that all students from all colleges got placed.
Q1. In KITM, 320 students were placed in at most 2 companies, which is 136 less than the number of students in HCTM who were placed in at least 5 companies. Find the ratio of total number of students in KITM and HCTM.
-
A. 3 : 5
B. 4 : 11
C. 2 : 3
D. 2 : 5
E. 3: 4
-
A. 105
B. 201
C. 160
D. 102
E. 120
-
A. LPU
B. GITM
C. MMU
D. HCTM
E. KITM
-
A. 2750
B. 2680
C. 2700
D. 2500
E. None of these
-
A. 448
B. 488
C. 484
D. 450
E. 438
1. The ratio of the volumes of two cubes is 729 : 1331. What is the ratio of their total surface areas?
- A. 81 : 121
B. 9 : 11
C. 729 : 1331
D. 27 : 121
- A. 140
B. 156
C. 175
D. 214
- A. 10
B. 100
C. 1000
D. 10000
- A. Rs. 3642.40
B. Rs. 3868.80
C. Rs. 4216.20
D. Rs. 4082.40
- A. 1 : 96
B. 1 : 48
C. 1 : 84
D. 1 : 68
Other Articles
 Study Guide
Study Guide
| Competitive Exams - Study Guide | ||
|---|---|---|
| Category | ||
| Quantitative Aptitude | Reasoning Ability | General Awareness |
| Computer Awareness | English Knowledge | Banking Awareness |
| General Science | World of Words | Descriptive Test |
 Exams
Exams
| Competitive Exams - Entrance Exams | |||
|---|---|---|---|
| Category | Notification | ||
| UG | NSTSE 2020 | RIMC Admission 2020 | WBJEE EVETS 2019 |
| Diploma | HPBOSE D.El.Ed CET 2019 | Goa Diploma Admissions 2019 | |
PG |
GATE 2020 |
ATMA 2019 |
XAT 2020 |
| Click Here For – All India Entrance Exam Notifications | |||
 Daily CA
Daily CA
 Job-Alerts
Job-Alerts
 SP Quiz
SP Quiz
| Competitive Exams - Practice Sets | |
|---|---|
| Category | Quiz |
| Quant Aptitude | Data Interpretation |
| Compound Interest | |
| Reasoning Ability | Puzzles |
| Insurance Awareness | Insurance Awareness |
 GK
GK
| General Knowledge for Competitive Examinations | |
|---|---|
| Topic | Name of the Article |
| GK - World | Women Leaders |
| Highest Civilian Awards | |
| GK - India | Indian Men Personalities |
| Indian River Projects | |
| GK - Abbreviations | Indian Railways Acronyms |
| Sports Abbreviations | |
| GK - Banking & Insurance | Insurance Ombudsman |
| Negotiable Instruments | |
| GK - Science & Technology | Physical Quantities and Units |
| Indian Research Institutes | |
| Famous Websites | |