Introduction
Introduction
Quantitative Aptitude is an important paper in banking exam. One cannot ignore it. So it is the most important to a candidate to improve the math’s skills for competitive exams. Most of the candidates feel that it’s a more time taking paper in exam but by following some guidelines, candidates can easily crack the exam. Competitive exams are setting with time binding. Everyone can do all maths without time binding but the main challenges are came into with in time. So candidates should mainly focus on speed and accuracy. That is possible in their hard working and Dedication. The article explains how to quickly calculate Last 2 Digits of Any Power Expression.
 Shortcut
Shortcut
How to find the last 2 digits of any power expression ([latex]a^{b}[/latex])
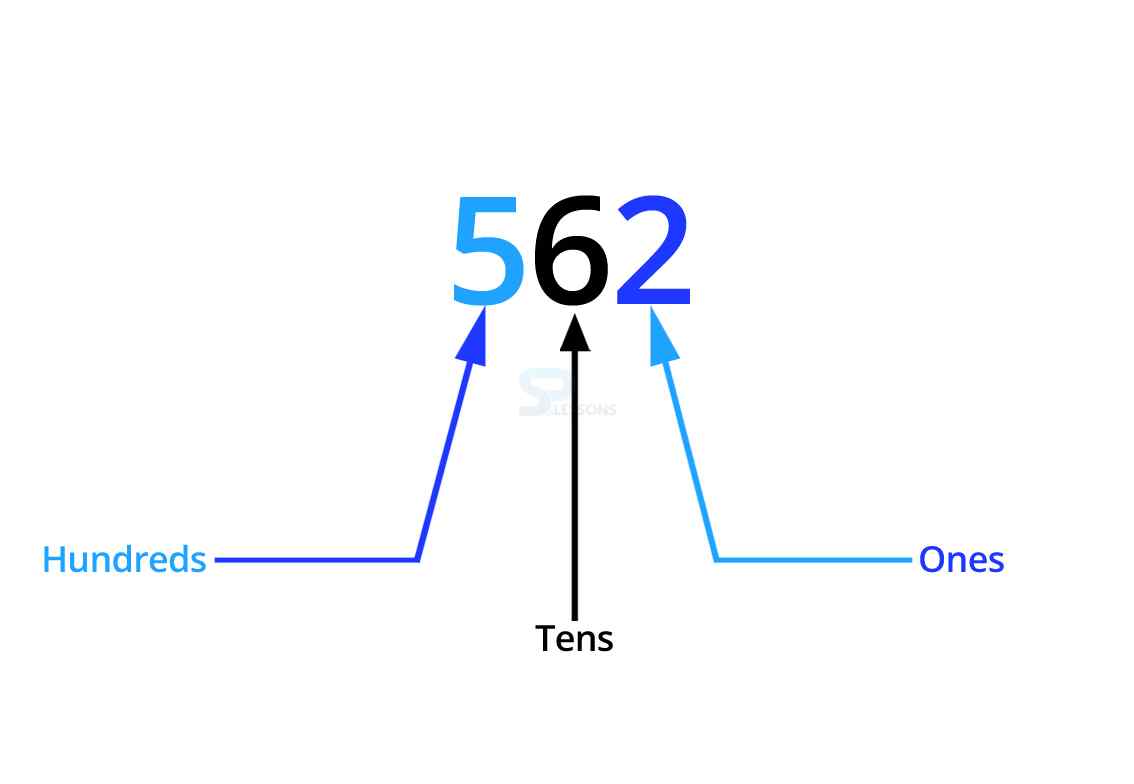
Before starting, let’s understand the meaning of ‘Ones’, ‘Tens’ and ‘Hundreds’. Look at the following number ‘562’.
The digit ‘5’ is in the Hundreds place, ‘6’ is in the Tens place, and ‘2’ is in the Ones place. The number 562 can be expanded as 5 × 100 + 6 × 10 + 2 × 1.
Similarly, numbers such as 2345 can be expanded as 2 × 1000 + 3 × 100 + 4 × 10 + 5 × 1. In this case, the digit ‘2’ is said to be in the Thousands place, ‘3’ to be in the Hundreds place, ‘4’ to be in the Tens place, and ‘5’ to be in the Ones place.
(Practice: What is the Ones and Hundreds digit of the number 3990?)
 Rules
Rules
Concept:
Given two numbers ‘a’ and ‘b’, we would like two know the last 2 digits of the number ‘c’ where c = [latex]a^{b}[/latex]. In simpler terms, we want to know what are the digits in the Ones and Tens place of the number c = [latex]a^{b}[/latex]. This is easy when the numbers ‘a’ and ‘b’ are small.
E.g: Calculating the number [latex]10^{2}[/latex], which is nothing but 100. So the last two digits (i.e. the Tens and Ones place digits) are 00. But this becomes difficult when we have to find out the last two digits of numbers like [latex]3456^{234}[/latex]. Let us learn the method to find out the last two digits of such numbers.
We will look at the following four sets:
I. When the number ‘a’ ends in 1: e.g. ‘a’ = 81
II. When the number ‘a’ ends in 3, 7 and 9: e.g. ‘a’ = 653 or ‘a’ = 817 or ‘a’ = 399
III. When the number ‘a’ ends in 2, 4, 6, 8: e.g. or ‘a’ = 72
IV. When the number ‘a’ ends in 5: e.g. ‘a’ = 55
It’s best to present the method with examples. We encourage you to follow the procedure on your own simultaneously on paper.
Before we learn the next set of cases, let us quickly look at the table of cyclicity of unit digits.
This table represents the cyclicity of the unit digits till power of 4. Observe that cyclicity of 2, 3, 7, and 8 is 3. Cyclicity of 4, and 9 is 1. Cyclicity of 0, 1, 5, and 6 is 0.
I. When the number ‘a’ ends in 1
Suppose we want to find the last two digits of the expression [latex]111^{2556}[/latex]. This means ‘a’ = 111 and ‘b’= 2556. Follow these steps now to get your answer.
Step 1: When ‘a’ ends with 1, the Ones digit of the answer will always be 1.
Step 2: Multiply the Tens digit of the number ‘a’ with the Ones digit of the ‘b’ (also called exponent). The Ones digit of this product will give the Tens digit of the answer.
From Step 1 we have, Ones digit as ‘1’. From Step 2, we have Tens digit as 1 (Tens digit of a) × 6 (Ones digit of b) = 6 (product). Therefore, the last two digits of [latex]111^{2556}[/latex] is 61.
Let’s see some more examples to make this clear.
Examples:
1) Find the last two digits of [latex]41^{8899}[/latex].
Solution: Here a = 41 and b = 8899. Since a is ending in 1, we have Ones digit of our answer as ‘1’. Next using Step 2, Tens digit is calculated as 4 (Tens digit of a) × 9 (Ones digit of b) = 36 (product). Pick the Ones digit of this Step. So, the solution is 61.
2) Find the last two digits of [latex]121^{45867}[/latex].
Solution: Here a = 121 and b = 45867. Since a is ending in 1, we have Ones digit of our answer as ‘1’. Next using Step 2, Tens digit is calculated as 2 × 7 = 14. Pick the Ones digit of this product, which is ‘4’. So, the solution is 41.
3) Find the last two digits of [latex]5145651^{456}[/latex] × [latex]61^{567}[/latex].
Solution: The last two digits of [latex]5145651^{456}[/latex] is 01 and the last two digits of [latex]61^{567}[/latex] is 21. Therefore last two digits of [latex]5145651^{456}[/latex] × [latex]61^{567}[/latex] is 01 × 21 that is 21.
| [latex]Digit[/latex] | [latex]Digit^{1}[/latex] | [latex]Digit^{2}[/latex] | [latex]Digit^{3}[/latex] | [latex]Digit^{4}[/latex] |
|---|---|---|---|---|
| 2 | 2 | 2 | 8 | 6 |
| 3 | 3 | 9 | 7 | 1 |
| 4 | 4 | 6 | ||
| 5 | 5 | |||
| 6 | 6 | |||
| 7 | 7 | 9 | 3 | 1 |
| 8 | 8 | 4 | 2 | 6 |
| 9 | 9 | 1 |
II. When the number ‘a’ ends in 3, 7 and 9: e.g. ‘a’ = 653 or ‘a’ = 817 or ‘a’ = 399
For this case, we have to change the unit digits 3, 7, and 9 to 1 by simple modifications. From Table 1, we can observe that 3, 7, and 9 may give Ones digit as 1 for the powers of 4, 4, and 2, respectively.
Suppose we want to find the last two digits of the expression [latex]1123^{2556}[/latex]. This means ‘a’ = 1123 and ‘b’ = 2556. Follow these steps now to get your answer.
Rewrite [latex]1123^{2556}[/latex] as [latex]23^{2556}[/latex] Why? Because, we are only interested only in the last two digits of the expression [latex]1123^{2556}[/latex].
Now, [latex]23^{64x4}[/latex] = [latex](23^{4})^{64}[/latex] = [latex](23^{2} × 23^{2})^{64}[/latex] = [latex] (529 × 529)^{64}[/latex].
Keep your focus only on the last two digits. This gives [latex](29 × 29)^{64}[/latex] = [latex](41)^{64}[/latex] (Because we are only interested in the last two digits!). So we finally reached to unit digit of ‘1’.
This means last two digits of [latex]1123^{2556}[/latex] is same as last two digits of [latex](41)^{64}[/latex]. Follow the steps in the first step, we get the last two digits of [latex](41)^{64}[/latex] as 61.
(Practice: Find the last two digits of [latex]657^{343}[/latex] ?)
III. When the number ‘a’ ends in 2, 4, 6, 8: e.g. or ‘a’ = 72
Let us now remember the following two rules to solve for this set.
Rule 1: [latex]2^{10}[/latex] raised to the even power always give last two digits as 76.
e.g. [latex]2^{260}[/latex] = [latex](2^{10})^{26}[/latex]. Therefore, last two digits of [latex]2^{260}[/latex] will be 76. The same holds true for [latex]2^{320}[/latex], that is, last two digits of [latex]2^{320}[/latex] will be 76.
Rule 2: [latex]2^{10}[/latex] raised to the odd power always give last two digits as 24. e.g. [latex]2^{70}[/latex] = [latex](2^{10})^{7}[/latex]. Therefore, last two digits of [latex]2^{70}[/latex] will be 24. The same holds true for [latex]2^{130}[/latex], that is, last two digits of [latex]2^{130}[/latex] will be 24.
Let us look at an example where we can utilize these rules. Suppose we would like to know the last two digits of [latex]36^{199}[/latex]. So, [latex]36^{199}[/latex] = [latex](2^{2} \times 3^{2})^{199}[/latex] = [latex]2^{2 × 199} × 3^{2 × 199}[/latex] = [latex]2^{398} × 3^{398}[/latex] = [latex]2^{(390+8)} × 3^{398}[/latex]. This is a good example to apply the above things we have learned.
A. [latex]2^{(390 + 8)}[/latex] = [latex]2^{390} × 2^{8}[/latex] = [latex](2^{10})^{39} × 256[/latex]. Keeping last two digits of [latex](2^{10})^{39} × 256[/latex], that is, 24 × 56. So, we get last two digits of [latex]2^{398}[/latex]equal to 44.
B. [latex]3^{398}[/latex] = [latex](3^{4})^{99} × 3^{2}[/latex] = [latex](81)^{99} × 9[/latex]. Keeping last two digits of [latex](81)^{99} × 9[/latex], that is, 21 × 09. So, we get last two digits of [latex]3^{398}[/latex] equal to 89.
Therefore, last two digits of [latex]36^{199}[/latex] = 44 × 89. Keeping last two digits of this, we get the answer as 16.
IV. When the number ‘a’ ends in 5: e.g. ‘a’ = 55
III. When the number ‘a’ ends in 5
The last two digits for numbers [latex]a^{b}[/latex], with a ending with ‘5’ are always 25 or 75.
Rule 1: If the product of Ones digit of the power b and digit left to the ‘5’ in a (Tens digit of a), is EVEN, then last two digits of the expression is 25.
Rule 2: If the product of ones digit of the power b and digit left to the ‘5’ in a (Tens digit of a), is ODD, then last two digits of the expression is 75.
Here’s an example for this set. We will calculate the last two digits of [latex]785^{587}[/latex]. Here a = 785 and b = 587. The Ones digit of b is 7 and Tens digit of a is 8. This means 7 × 8 is 56 which is EVEN. Therefor the last two digits of [latex]785^{587} [/latex] is 25. Similarly, the last two digits of [latex]1475^{589}[/latex] is 75.
 Exercises
Exercises
1. Find the last two digits of [latex]234^{876}[/latex].
2. Find the last two digits of [latex]47^{4544}[/latex].
3. Find the last two digits of [latex]7^{2008}[/latex].
Answers:
1. 16
2. 41
3. 01