1. Points:

• In geometry, points help to determine exact locations.


• Points are generally represented by a number or letter.


• Since points determine a single, exact locations (but are not objects in themselves), they are zero-dimensional.


• In other words points have no length, width, or height.


• They just show up as items when drawn on a paper.

2. Rays:

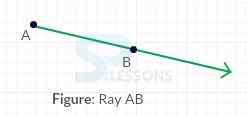
• A ray is a "straight" line that starts at one point and develops infinitely in one direction.


• A ray has one endpoint, which denote the position from where it starts.


• A ray starting at the point A that goes through point B is indicated as [latex]\overrightarrow{AB}[/latex].


• This representation demonstrates that the ray starts at point A and broadens infinitely toward point B.

3. Lines:

• Lines in geometry might be considered as a "straight" line that can be drawn on paper with a pencil and ruler.


• Rather than this line being limited by the measurements of the paper, a line expands limitlessly in both directions.


• A line is one-dimensional, having length, however, no width or height.


• Lines are uniquely determined by two points.


• Therefore, the name of a line going through the points A and B is represented as [latex]\overleftrightarrow{AB}[/latex], where the two-headed arrow implies that the line goes through those unique points and extends endlessly in both directions.

4. Line segment:

• Lines and line segments differ because a line segment has a defined length, whereas a line does not.


• It is represented as [latex]\overline{AB}[/latex].

5. Intersection:

From the above figure, point D is the point of intersection.

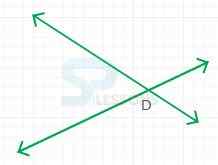
• The term intersect is used when lines, rays, line segments or figures meet, that is, they share a common point.


• The point they share is called the point of intersection.

6. End points:

• An end point is a point used to define a line segment or ray.


• A line segment has two endpointd whereas a ray has one end point.

7. Parallel lines:

• Two lines in the same plane which never intersect are known as parallel lines.


• Two line segments are parallel if the lines that they lie on a parallel.


• If [latex]L_{1}[/latex] is parallel to [latex]L_{2}[/latex], then it is represented as [latex]L_{1} \parallel L_{2}[/latex].

8. Angles:

• An angle is framed when two rays meet at a typical endpoint, or vertex.


• The two sides of the angle are the rays, and the point that joins them is known as the vertex.

Acute angles:

• An acute angle is an angle whose measure is less than 90°.


• For these sorts of points, a square couldn't fit splendidly at the convergence of the two lines that frame them.

Obtuse angles:

• Obtuse angles have measures greater than 90° but less than 180°.

Complementary angles:

• Two angles are known as complementary if the sum of their degree measurements equals 90 degrees.


• One of the complimentary angles is said to be complement of the other.

Supplementary angles:

• Two angles are known as supplementary if the sum of their degree measurements equals 180 degrees.


• One of the supplementary angles is said to be supplement of the other.

Vertically opposite angles:

• When two lines intersect, the angles that lie opposite to each other called vertically opposite angles, are always equal.

9. Angle bisector:

From the above figure, line segment OB is the angular bisector.

• An angle bisector is a ray that divides an angle into two equal angles.

10. Perpendicular lines:

From the above figure, AB and CD lines are perpendicular to each other.

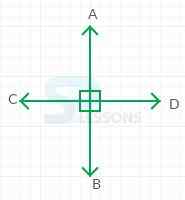
• Lines are perpendicular if their intersection forms a right angle and if one of the angles formed by the intersection of two lines or segments is a right angle, then all four angles created will also be right angles.


• This also shows that the degree measurement of four angles formed by two intersecting lines will add up to 360 degrees.

11. Parallel lines cut by a traversal:

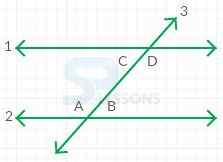
• A traversal creates eight angles when it intersects with two parallel lines.


• The eight angles created by these two intersections have special relationships to each other.

Alternate interior angles:

• For any pair of parallel lines 1 and , that are both intersected by a third line, such as line 3 in the figure shown.


• Angle A and angle D are called alternate interior angles.


• Alternate interior angles have the same degree measurement.


• Angle B and angle C are also alternate interior angles.

Alternate exterior angles:

• For any pair of parallel lines 1 and , that are both intersected by a third line, such as line 3 in the figure shown.


• Angle A and angle D are called alternate exterior angles.


• Alternate exterior angles have the same degree measurement.


• Angle B and angle C are also alternate interior angles.

Corresponding angles:

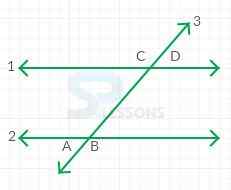
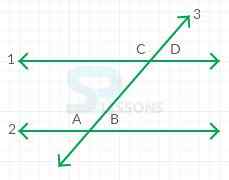
• For any pair of parallel lines 1 and , that are both intersected by a third line, such as line 3 in the figure shown.


• Angle A and angle C are called corresponding angles.


• Corresponding angles have the same degree measurement.


• Angle B and angle D are also corresponding angles.

12. Polygon:

• A polygon is a closed figure made by joining line segments, where each line segment intersects exactly two others.

Eg: The following are examples of polygons:

Regular polygon:

• A regular polygon is a polygon whose sides are all the same length, and whose angles are all the same.

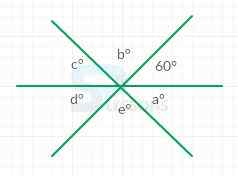
1. In the figure below, if [latex]c[/latex] = 2[latex]e[/latex]. Then find the angle [latex]b[/latex].

Solution:

Given that
[latex]c[/latex] = 2[latex]e[/latex]
From the figure,
The angle opposite to [latex]d^{\circ}[/latex] is [latex]{60}^{\circ}[/latex]
So, [latex]d^{\circ}[/latex] = [latex]{60}^{\circ}[/latex]
[latex]c + d + e[/latex] = [latex]{180}^{\circ}[/latex]
⇒ [latex]2e + d + e[/latex] = [latex]{180}^{\circ}[/latex]
⇒ [latex]c + d + e[/latex] = [latex]{180}^{\circ}[/latex]
⇒ [latex]3e[/latex] = [latex]{180}^{\circ}[/latex]
⇒ [latex]e[/latex] = [latex]{40}^{\circ}[/latex]
Since [latex]b[/latex] and [latex]c[/latex] are vertically opposite angles
[latex]\angle b[/latex] = [latex]\angle c[/latex] = [latex]{40}^{\circ}[/latex]
Therefore, [latex]\angle b[/latex] = [latex]{40}^{\circ}[/latex]

2. Line XY is parallel to line WZ and angle A is 105 degrees. Find the measurement of angle H in degrees?
Solution:

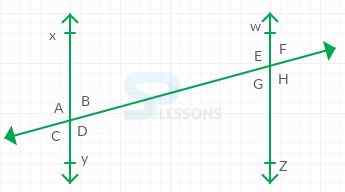
Given that
Line XY is parallel to line WZ.
[latex]\angle A[/latex] = [latex]{105}^{\circ}[/latex]



Since, line XY is parallel to line WZ then measurements of angle A and angle E are equal to each other because they are corresponding angles.
The measurements of angles E and H are also equal to each other because they are vertical angles.
Therefore, [latex]\angle H[/latex] = [latex]{105}^{\circ}[/latex].

3. Line DE is parallel to line BC, angle 2 is equal to angle 3, and angle 1 is right angle. What is the measure of angle 5 in degrees?

Solution:

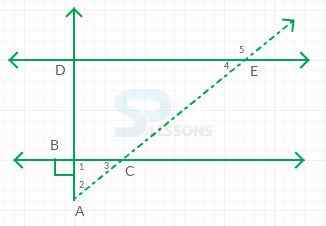
Given that
Line DE is parallel to line BC.
Since triangle ABC is a right triangle, angles 2 and 3 are equal.
Sum of three angles in a triangle = [latex]{180}^{\circ}[/latex].
Therefore angles 2 and 3 are both [latex]{45}^{\circ}[/latex].
Since line DE is parallel to line BC, then the measurements of angle 3 and angle 4 are equal to each other because they are corresponding angles.
Angles 4 and 5 make up a straight angle, so their sum = [latex]{180}^{\circ}[/latex].
So, angle 5 would be 180 - 45 = 135 degrees.

4. QRS is an isosceles triangle with angles Q = [latex]{45}^{\circ}[/latex] and R = [latex]{45}^{\circ}[/latex] and line segments QS = 8 and QR = [latex]x[/latex]. Polygon DEFGH has sides DE = 3 and GH = [latex]y[/latex] and polygon LMNOP has sides LM = 1 and OP = 2.
A. The quantity on the left is greater. B. The quantity on the right is greater. C. Both are equal. D. The relationship cannot be determined without further information.
Solution:

The problem does not state that polygons DEFGH and LMNOP are similar.
There is no information representing that their corresponding sides are in the same ratio or that corresponding angles are equal, this cannot be determined.
There is not enough information to solve the problem.
Hence correct option is D.

5: A. The quantity on the left is greater. B. The quantity on the right is greater. C. Both are equal. D. The relationship cannot be determined without further information.
Solution:

No. of diagonal in a polygon of side [latex]n[/latex] is [latex]\frac{n(n - 3)}{2}[/latex]
so, no. of diagonal in a decagon is [latex]\frac{10(10 - 3)}{2}[/latex] = 35
Hence, correct option is B.