Types of quadrilaterals:
Rectangle: A four sided polygon having all right angles is known as rectangle. The sum of the angles of a rectangle is 360 degrees. (or)
A rectangle is a parallelogram with four right angles, two pairs of congruent opposite sides, and two congruent diagonals.

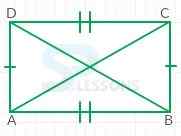
From the above figure,

• [latex]\overline{AB} \parallel \overline{DC}[/latex]


• [latex]m \overline{AB}[/latex] = [latex]m \overline{DC}[/latex]


• [latex]m \overline{AC}[/latex] = [latex]m \overline{BD}[/latex]


• [latex]m\angle[/latex]A = [latex]m\angle[/latex]B = [latex]m\angle[/latex]C = [latex]m\angle[/latex]D = [latex]{90}^{\circ}[/latex]

Properties of rectangle:

• All four angles of a rectangle are right angles.


• The diagonals of a rectangle are congruent.

The perimeter of a rectangle is twice the sum of its length and width i.e.
Perimeter = 2([latex]a[/latex] + [latex]b[/latex])
The area is the product of the length and width i.e.
Area = [latex]a[/latex] x [latex]b[/latex]
Square:
Rectangle of equal sides is known as a square.
(OR)
A square is a parallelogram with four congruent sides and four congruent angles.

From the figure above,

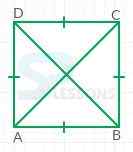
• [latex]\overline{AB} \parallel \overline{DC}[/latex]


• [latex]m \overline{AB}[/latex] = [latex]m \overline{DC}[/latex]


• [latex]m \overline{AC}[/latex] = [latex]m \overline{BD}[/latex]


• [latex]m\angle[/latex]A = [latex]m\angle[/latex]B = [latex]m\angle[/latex]C = [latex]m\angle[/latex]D = [latex]{90}^{\circ}[/latex]

If the side of the square is [latex]a[/latex], then
The perimeter of a square = [latex]a[/latex] + [latex]a[/latex] + [latex]a[/latex] + [latex]a[/latex] = 4[latex]a[/latex]
Area of a square = [latex]a[/latex] x [latex]a[/latex] = [latex]a^2[/latex]

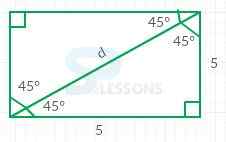
• Diagonals bisect each other at right angles and are equal in length.


• Diagonals bisect the vertex angles to create [latex]{45}^{\circ}[/latex] angles.


• Formula for the area of a square is A = [latex]a^2[/latex].


• formula for perimeter of a square is P = 4[latex]a[/latex].

For example, let [latex]a[/latex] is the length of a side of square.
If length is known, calculating the length of the diagonal is easy i.e.

From the above figure,
Since [latex]d[/latex] is the hypotenuse of the 45-45-90 triangle which has legs of length 5,
according to the ratio 1 : 1 : [latex]\sqrt{2}[/latex]
Hence, diagonal [latex]d[/latex] = 5[latex]\sqrt{2}[/latex].
Parallelogram: Parallelogram is a convex quadrilateral with one pairs of parallel sides. Altitude (or height) is the segment perpendicular to the base. Special parallelograms are rectangles, squares and rhombuses.

From the above figure,
Perimeter of a parallelogram is the sum of its sides i.e.
Perimeter = [latex]a[/latex] + [latex]b[/latex] + [latex]a[/latex] + [latex]b[/latex] = 2([latex]a[/latex] + [latex]b[/latex])
The area is the product of the base and height i.e.
Area = [latex]b[/latex] x [latex]h[/latex]
Rhombus: A four-sided polygon having all four sides of equal length is known as rhombus. The sum of the angles of a rhombus is 360 degrees.
(OR)
A rhombus is a parallelogram with two pairs of congruent opposite angles, four congruent sides, and two perpendicular diagonals that bisect the angles of a rhombus.

From the above figure,

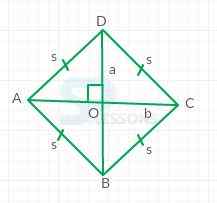
• [latex]\overline{AB} \parallel \overline{DC}[/latex]


• [latex]m \overline{AB}[/latex] = [latex]m \overline{BC}[/latex] = [latex]m \overline{CD}[/latex] = [latex]m \overline{DA}[/latex]


• [latex]\overline{AD} \parallel \overline{BC}[/latex]


• [latex]AC \perp BC[/latex]


• [latex]m\angle[/latex]A = [latex]m\angle[/latex]C


• [latex]m\angle[/latex]ABO = [latex]m\angle[/latex]CBO =[latex]m\angle[/latex]ADO = [latex]m\angle[/latex]CDO


• [latex]m\angle[/latex]B = [latex]m\angle[/latex]D


• [latex]m\angle[/latex]BAO = [latex]m\angle[/latex]DAO =[latex]m\angle[/latex]BCO = [latex]m\angle[/latex]DCO

The perimeter of a rhombus is the quadruple of its side i.e.
Perimeter = [latex]s[/latex] + [latex]s[/latex] + [latex]s[/latex] + [latex]s[/latex] = 4[latex]s[/latex]
The area is the product of the diagonals i.e.
Area = [latex]\frac{a * b}{2}[/latex]
Trapezoid:

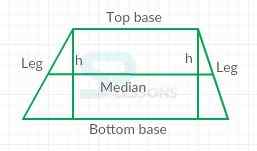
• Trapezoid is a convex quadrilateral with exactly one pair of parallel sides.


• Bases are the parallel sides, and the legs are non parallel sides.


• Altitude (or height) is the segment perpendicular to the bases.


• Median is the segment connecting the mid points of the legs.





• Trapezoid with congruent legs is an isosceles trapezoid. Since legs are congruent, both pairs of the base angles are also congruent.


• The sum of the measures of the four interior angles is always 360 degrees. Further more, the same side interior angles between the bases are supplementary.
  [latex]m\angle[/latex]A + [latex]m\angle[/latex]B + [latex]m\angle[/latex]C + [latex]m\angle[/latex]D = [latex]{360}^{\circ}[/latex]
  [latex]m\angle[/latex]A + [latex]m\angle[/latex]D = [latex]{180}^{\circ}[/latex]
  [latex]m\angle[/latex]B + [latex]m\angle[/latex]C = [latex]{180}^{\circ}[/latex]

The perimeter of a trapezoid is the sum of its sides i.e.
Perimeter = [latex]a[/latex] + [latex]b[/latex] + [latex]c[/latex] + [latex]d[/latex].
The area of a trapezoid is one half of the product of its height and the sum of bases i.e.
Area = [latex]\frac{1}{2}[/latex] x ([latex]b[/latex] + [latex]d[/latex]) x [latex]h[/latex].

1. Rectangle: Perimeter = 2([latex]a[/latex] + [latex]b[/latex]) Area = [latex]a[/latex] x [latex]b[/latex]
2. Square: Perimeter = [latex]a[/latex] + [latex]a[/latex] + [latex]a[/latex] + [latex]a[/latex] = 4[latex]a[/latex] Area = [latex]a[/latex] x [latex]a[/latex] = [latex]a^2[/latex]
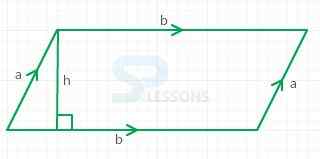
3. Parallelogram: Perimeter = [latex]a[/latex] + [latex]b[/latex] + [latex]a[/latex] + [latex]b[/latex] = 2([latex]a[/latex] + [latex]b[/latex]) Area = [latex]b[/latex] x [latex]h[/latex]
4. Rhombus: Perimeter = [latex]s[/latex] + [latex]s[/latex] + [latex]s[/latex] + [latex]s[/latex] = 4[latex]s[/latex] Area = [latex]\frac{a * b}{2}[/latex]
5. Trapezoid: Perimeter = [latex]a[/latex] + [latex]b[/latex] + [latex]c[/latex] + [latex]d[/latex] Area = [latex]\frac{1}{2}[/latex] x ([latex]b[/latex] + [latex]d[/latex]) x [latex]h[/latex]

1. If the length of rectangle A is one-half the length of rectangle B, and the width of rectangle A is one-half the width of rectangle B, what is the ratio of area of rectangle A to the area of rectangle B?
Solution:

Given that,
The length of rectangle A is one-half the length of rectangle B.
The width of rectangle A is one-half the width of rectangle B.
The ratio of areas is not the same as the ratio of lengths. Instead, the ratio of areas for similar polygons is equal to the square of the lengths of the lengths.
If the length and width of a rectangle are 4 and 2, then its area = 8.
Rectangle B would have area of 8 x 4 = 32 four times that of A.

2 Sally is mounting photographs on matting board. She has 48 square inches of matting board to work with and stack of five rectangular photos each measuring 3 x 5. Assume that she is cutting the board to fit each photo exactly, with no board wasted.

I. Number of photos she can mount.
II. Number of photos she does not have enough board to mount.

Solution:

Given that,
Sally has 48 square inches of matting board to work with.
Stack of five rectangular photos each measuring 3 x 5.
Each photo require 15 sq. inch of mounting board since A = [latex]lw[/latex] = 3 x 5 = 15.
Where, [latex]l[/latex] is length and [latex]w[/latex] is width.
I. Number of photos she can mount:
If three photos are mounted, then 15 x 3 = 45 sq.in. of matting board.
II. Number of photos she does not have enough board to mount:
Since Sally started with 48 sq. in. of board,
Using 45 sq.in. in will leave her 3 sq.in. left over which is not enough to mount a fourth photo.
Mounting 3 of five photos will leave her with 2 unmounted photos.

3. Max intends to tile a kitchen floor, which is 9 ft by 11 ft. How many 6-inch tiles are needed to tile the floor?
Solution:

Tiles are measured in inches, so convert the area of the floor to inches as well.
The length of the floor is 9 ft x 12 inch per foot = 108 inch.
The width of the floor is 11 ft x 12 inch per foot = 132 inch.
Area of rectangle = length x width.
Therefore, area of kitchen floor is 108 inch x 132 inch or 14,256 sq.inch.
Area of one tile is 6 inch x 6 inch or 36 sq.inch.
Therefore, divide the total number of square inches by 36 sq. inch or 14,256 sq.inch divided by 36 sq.inch = 396 tiles.

4.
A. The quantity on the left is greater. B. The quantity on the right is greater. C. Both are equal. D. The relationship cannot be determined without further information.
Solution:

Length and breadth are not given.
Length and breadth could be any thing only thing is their double of sum should be 12.
So, it is impossible to calculate perimeter.
The given information is insufficient to solve the problem.
Hence, option B is correct one.

5. Mr. Jenkins is installing a pool in his backyard. The pool will be in form of rectangle with a length of 12 feet and a width of 8 feet. There will also be a 36 sq. foot wooden deck built adjacent to one side of the pool.
A. The quantity on the left is greater. B. The quantity on the right is greater. C. Both are equal. D. The relationship cannot be determined without further information.
Solution:

Given that
Length = 12 feet and
Width = 8 feet
Area of rectangle (A) = [latex]lw[/latex]
A = 12 x 8
A = 96 sq. ft.
Now, add area of deck to this area i.e. 36 + 96 = 132 sq. ft.
132 sq. ft is more than value of quantity A i.e. 120 sq. ft.
Hence, correct option is B.