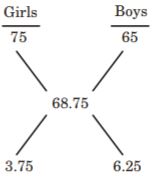
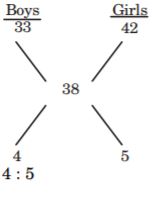
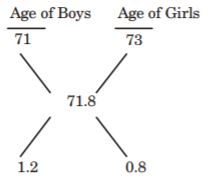
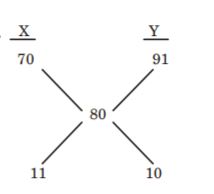
Introduction
Introduction
The article Average Practice Quiz is useful for candidates preparing for different competitive examinations like RRB ALP/Technical Exams/Junior Engineer Recruitment Exams, SSC, IBPS PO Exams and etc.
The Average (arithmetic mean) of a group or set of N numbers is defined as the sum of those numbers divided by N. Here N is the number of values or observations in a set
Average = [latex]\frac{Sum of N numbers/values}{Numbers of values/observations}[/latex]
A = [latex]\frac{Sum}{N}[/latex] or Sum = N * Average
 Quiz
Quiz
1. A man cover s a certain distance at 90 km/hr and returns back to the starting point at 60 km/hr. His average speed during the whole journey is
- A. 60 km/hr
B. 65 km/hr
C. 72 km/hr
D. 75 km/hr
- A. 18 kmph
B. 22 kmph
C. 24 kmph
D. 26 kmph
- A. 20
B. 22
C. 17
D. 19
- A. 10 kmph
B. 20 kmph
C. 25 kmph
D. 30 kmph
- A. 20
B. 28
C. 30
D. 32
- A. 33
B. 36
C. 38
D. 40
- A. [latex]\frac{200}{3}[/latex]
B. 40
C. [latex]\frac{50}{9}[/latex]
D. [latex]\frac{400}{9}[/latex]
- A. 20
B. 25
C. 40
D. 60
- A. 30 kmph
B. 42.86 kmph
C. 55 kmph
D. 60 kmph
- A. [latex]\frac{200}{11}[/latex]
B. [latex]\frac{400}{11}[/latex]
C. [latex]\frac{500}{11}[/latex]
D. [latex]\frac{600}{11}[/latex]
- A. 4 km/hr
B. 4.5 km/hr
C. 5 km/hr
D. 3 km/hr
- A. 22.25
B. 24.25
C. 25
D. 25.5
- A. 850.5
B. 858.5
C. 854.5
D. 852.5
- A. 51
B. 50
C. 49.5
D. 49
- A. 106
B. 105
C. 104
D. 107
1. Find the average of all prime numbers between 30 and 50 :
- A. 48
B. 39
C. 39.8
D. 38
- A. 12 years
B. 4 years
C. 8 years
D. 15 years
- A. 48
B. 58
C. 60
D. 78
- A. 180
B. 190
C. 200
D. 210
- A. 3.6
B. 4.5
C. 5.5
D. 5.6
- A. 35
B. 40
C. 45
D. 50
- A. 5
B. 6
C. 7
D. 8
- A. 65.5
B. 65.3
C. 65.6
D. 65.8
- A. 40
B. 45
C. 50
D. 60
- A. 9
B. 30
C. 10.67
D. 60
- A. 6
B. 7.5
C. 9
D. 11
- A. 5.4
B. 5.8
C. 6.8
D. 7.8
- A. 35.5
B. 35
C. 36
D. 36.5
- A. 8
B. 7
C. 6
D. 3
- A. 26
B. 27
C. 27.5
D. 28
1. If 12a + 6b = 54, what is the average of a & b?
- A. 2.25
B. 4.5
C. 6
D. Data insufficient
- A. 2 : 5
B. 5 : 2
C. 3 : 5
D. 5 : 3
- A. 4.6
B. 4.7
C. 4.8
D. 4.5
- A. 37.5
B. 42.5
C. 45
D. 50.5
- A. 203
B. 201
C. 202.5
D. 203.5
- A. X
B. [latex]\frac{n}{2} + 1[/latex]
C. [latex]\frac{n(n + 1)}{2} [/latex]
D. [latex]\frac{(n + 1)}{2} [/latex]
- A. 44 [latex]\frac{4}{9}[/latex]
B. 46 [latex]\frac{5}{9}[/latex]
C. 55 [latex]\frac{5}{9}[/latex]
D. 55 [latex]\frac{4}{9}[/latex]
- A. 35
B. 40
C. 60
D. 80
- A. [latex]\frac{11}{10}[/latex]
B. [latex]\frac{33}{10}[/latex]
C. [latex]\frac{24}{5}[/latex]
D. [latex]\frac{26}{5}[/latex]
- A. [latex]\frac{n(n - 1)}{2}[/latex]
B. [latex]\frac{(n + 1)}{2}[/latex]
C. [latex]\frac{n(n + 1)}{2}[/latex]
D. [latex]\frac{(n - 1)}{2}[/latex]
- A. 67
B. 72
C. 73
D. 89
- A. 25.5
B. 50
C. 50.5
D. 60
- A. 37.5
B. 62.5
C. 60
D. 65
- A. 27
B. 29
C. 31
D. 33
- A. 80
B. 90
C. 100
D. 120