Introduction
Introduction
Number System is all about finding the face value & place value of a digit, basic rules and different types of numbers, rules for divisibility, factors and multiples. Number System is one of the important topic in the Quantitative Aptitude section . Number system is a system to represent numbers using digits and symbols. Number system provides a unique representation of every number and represents arithmetic and algebraic structure of the figures.
Quantitative Aptitude -BANKING|SSC|RAILWAYS|INSURANCE|RECRUITMENT EXAMS - EBOOKS
 Methods
Methods
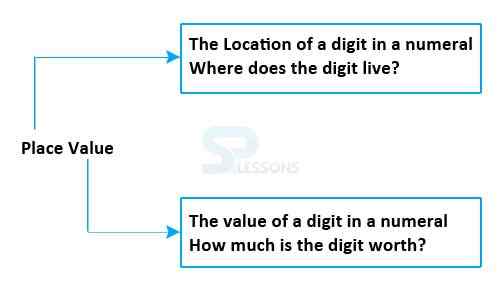
Face Value -
Face Value of the digit in numeral is the value of digit itself, irrespective of its place in the numeral.
For example, In the numeral 36578,
- The face value of 8 is 8
- The face value of 7 is 7
- The face value of 5 is 5
- The face value of 6 is 6
- The face value of 3 is 3
| Crores | Ten Lakhs | Lakhs | Ten Thousands | Thousands | Hundreds | Tens | Ones |
|---|---|---|---|---|---|---|---|
| 3 | 6 | 5 | 7 | 8 |
- Place value of 8 = (8 x 1) = 8, (Here, to get the place value of 8, we multiply 8 by 1. Because 8 is at Ones place)
- Place value of 7 = (7 x 10) = 70, (Here, to get the place value of 7, we multiply 7 by 10. Because 7 is at Tens place)
- Place value of 5 = (5 x 100) = 500, (Here, to get the place value of 5, we multiply 5 by 100. Because 5 is at Hundreds place)
- Place value of 6 = (6 x 1000) = 6000, (Here, to get the place value of 6, we multiply 6 by 1000. Because 6 is at Thousands place)
- Place value of 3 = (3 x 10000) = 30000, (Here, to get the place value of 3, we multiply 3 by 10000. Because 3 is at Ten Thousands place)
-
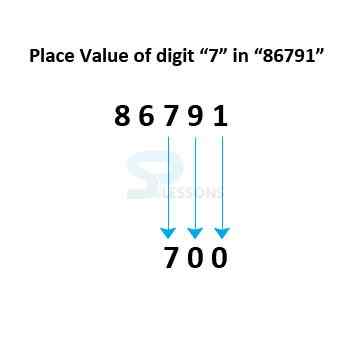
As per the Place, the location of “3” in 36578 is Ten Thousands place.
As per the Value, the value of “3” in 36578 is 30000.
Finally, the place value of "3" in 36578 is "30000"
- In the number above, 5 is underlined.
The face value of 5 is the same.
So, the face value of 5 is 5.
To get place value, count the number of digits after 5.
There is only one digit after 5.
So, the place value of 5 is 50.
- From the given information, let us find the value of "K".
K = 2x = 2(4) = 8 → K = 8
so, we have
K25937 → 825937
To get place value of "K", we have to count the number of digits after “8”.
There are five digits after 8.
Hence, the place value of "K" is 800000.
- From the given information, let us find the value of "K".
K = 6
(Because 6 is the only number less than 10 and also exactly divisible by both 2 and 3)
So, we have
58K32 → 58632
To get place value of "K", we have to count the number of digits after 6.
There are two digits after 6.
Hence, the place value of "K" is 600.
- Natural numbers are defined as the numbers that occur commonly in nature. A natural number is a whole, non negative number and the set of natural numbers is denoted by letter 'N'. Set of natural numbers is N = {1,2,3.....}
- Whole numbers are defined as all the numbers without fractions and no decimals.
Set of whole numbers is (W)={0,1,2,3.......}
Note: Every natural number is a whole number except zero is a whole number which is not a natural number.
- Integers are defined as all the numbers i.e. zero, positive and negative numbers. Set of integers = {......-3,-2,-1,0,1,2,3,.......}
- Even numbers are defined as the numbers divisible by 2. i.e When an even number is divided by 2, the remainder is 0. 0,2,4,6,..... are even numbers.
- Odd numbers are defined as the numbers which are not divisible by 2. i.e When an even number is divided by 2, the remainder is 1. 1,3,5,7,...... are odd numbers.
- Prime numbers are those numbers which have exactly two factors namely itself and 1. Example: 2,3,5,7,11,13,17....etc.
- Composite numbers are defined as the numbers which are not prime. Example: 4,6,8,12,15,..... etc.
- Divisibility by 2: A number is divisible by 2 if the last digit in a given numerical value is 0,2,4,6,8. Example: 526492 is divisible by 2. (as last digit is 2)
- Divisibility by 3: A number is divisible by 3 if the sum of its digits is divisible by 3. Example: 562185 is divisible by 3. (as sum of digits =27 is divisible)
- Divisibility by 4: If the number formed by last two digits is divisible by 4 then the given numerical value is also divisible by 4. Example: 1459872 is divisible by 4. (as last two digits 72 is divisible by 4)
- Divisibility by 5: If the units digit is 0 or 5, then the given number is divisible by 5. Example: 256480 is divisible by 5. (as units digit is 0)
- Divisibility by 8: If the number formed by last three digits is divisible by 8 then the given numerical value is also divisible by 8. Example: 45566568 divisible by 8. (as 568(the number formed by last 3 digits) is divisible by 8)
- Divisibility by 9: If the sum of its digits is divisible by 9 then the given numerical value is also divisible by 9. Example: 21421899 divisible by 9. (as sum of its digits = 36 is divisible by 9)
- Divisibility by 10: If the units digit is 0, then the given number is divisible by 10. Example: 65712590 is divisible by 10. (as units digit is 0)
- Divisibility by 11: If the difference between sum of its digits at odd places and sum of its digits in even places is either zero or a number divisible by 11. Example: 25784 is divisible by 11. (as (2+ 7 + 4) - (5+8) = 13 - 13 =0)
Formula 1: Dividend = (Quotient x Divisor) + Remainder
Explanation:
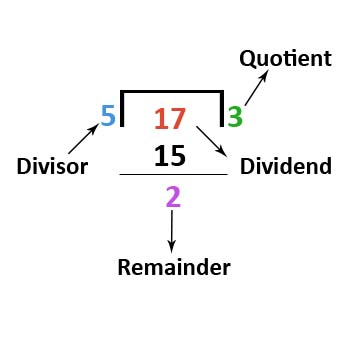
When dividing a number by another number, one will have the terms dividend, divisor, quotient and remainder.
- The number which we divide is called the dividend.
- The number by which we divide is called the divisor.
- The result obtained is called the quotient.
- The number left over is called the remainder.
- 17 = 5 x 3 + 2
Where;
- 17 - Dividend
- 3 - Quotient
- 5 - Divisor
- 2 - Remainder
- If 300 divided by 7 using long division.
- Dividend - 300
- Divisor - 7
- Quotient - 42
- Remainder - 6
- If 400 divided by 8 using long division:
- Dividend = 400
- Divisor = 8
- Quotient = 50
- Remainder = 0
- If 750 divided by 16 using long division:
- Dividend = 750
- Divisor = 16
- Quotient = 46
- Remainder = 14
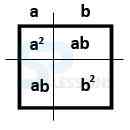
Formula 2: Why is [latex](a+b)^2 = a^2 + b^2 +2ab[/latex]
Explanation: This is the first formula in geometry and algebra of mathematics.
- Introduction to Geometrical Approach:
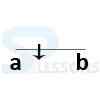
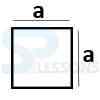
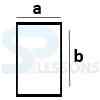
- Line with a point = a+b
- Square Area = [latex]a^{2}[/latex]
- Rectangle Area = ab
- Draw a line with a point which divides a, b
- Total distance of this line = a+b
- Now find out the square of a+b ie. [latex](a+b)^{2}[/latex]
- The above diagram represents – a + b is a line and the square are is [latex]a^{2}[/latex] + [latex]b^{2}[/latex] + 2ab
- [latex](3x + 4y)^{2}[/latex] = [latex](3x)^{2}[/latex] + [latex](4y)^{2}[/latex] + 2(3x)(4y) = [latex]9x^{2}[/latex] + [latex]16y^{2}[/latex] + 24xy
∴ [latex](3x + 4y)^{2}[/latex] = [latex]9x^{2}[/latex] + [latex]16y^{2}[/latex] + 24xy
- [latex](\sqrt{2}x + 4y)^{2}[/latex] = [latex](\sqrt{2}x)^{2}[/latex] + [latex](4y)^{2}[/latex] + 2[latex](\sqrt{2}x)[/latex](4y) = [latex]2x^{2}[/latex] + [latex]16y^{2}[/latex] + 8[latex]\sqrt{2}[/latex]xy
∴ [latex](\sqrt{2}x + 4y)^{2}[/latex] = [latex]2x^{2}[/latex] + [latex]16y^{2}[/latex] + 8[latex]\sqrt{2}[/latex]xy
- [latex](x + \frac{1}{x})^{2}[/latex] = [latex]x^{2}[/latex] + [latex]\frac{1}{x^{2}}[/latex] + 2[latex](x)(\frac{1}{x})[/latex] = [latex]x^{2}[/latex] + [latex]\frac{1}{x^{2}}[/latex] + 2
∴ [latex](x + \frac{1}{x})^{2}[/latex] = [latex]x^{2}[/latex] + [latex]\frac{1}{x^{2}}[/latex] + 2
Formula 3: Prove that [latex](1+2+3+....+n) = \frac{1}{2n(n+1)}[/latex] for n, n is natural number.
Explantion:
Step: 1
- Prove for n = 1
1 = [latex]\frac{1}{2}[/latex]n(n + 1)
1 = [latex]\frac{1}{2}[/latex].1.(1 + 1)
1 = [latex]\frac{1}{2}[/latex].1.2
1 = 1, proved to be true
- Prove for n = k
1 + 2 + 3 + …. + K = [latex]\frac{1}{2}[/latex] k (k + 1), is true, so for n = k + 1 it is also true
1 + 2+ 3 + … + k + k + 1 = [latex]\frac{1}{2}[/latex] (k + 1) ((k+1) + 1)
(1 + 2 + 3 + … + k) + k + 1 = [latex]\frac{((k + 1) (k + 2))}{2}[/latex]
( [latex]\frac{1}{2}[/latex] k (k + 1)) + K + 1 = [latex]\frac{((k + 1) (k + 2))}{2}[/latex]
[latex]\frac{((k + 1) (k + 2))}{2}[/latex] = [latex]\frac{((k + 1) (k + 2))}{2}[/latex], proved to be true
Because Step 1 and Step 2 are true, so it can be concluded that the statement is true.
 Formulae
Formulae
- (Divisor × Quotient) + Remainder = Dividend
- [latex](a+b)^2 = a^2 + b^2 +2ab[/latex]
- [latex](a-b)^2 = a^2 + b^2 -2ab[/latex]
- [latex]a^2 - b^2 = (a+b)(a-b)[/latex]
- [latex](1+2+3+....+n) = \frac{1}{2n(n+1)}[/latex]
- [latex]1^2+2^2+3^2+....+n^2 = \frac{1}{6n(n+1)(2n+1)}[/latex]
- [latex]1^3+2^3+3^2+....+n^3 = \frac{1}{4n^2(n+1)^2}[/latex]
- For Arithmetic Progression (i) nth term = [latex]a + (n - 1)d[/latex] (ii) sum of n terms = [latex]\frac{n}{2(2a+(n-1)d)}[/latex] (iii) sum of n terms = [latex]\frac{n}{2(a+l)}[/latex], where l is the last term
- For Geometric Progression (i) nth term = [latex]ar^{(n-1)}[/latex] (ii) sum of n terms = [latex]\frac{a(1-r^n)}{(1-r)}[/latex] when r<1 ; [latex]\frac{a(r^n-1)}{(r-1)}[/latex] when r>1
 Samples
Samples
1. Find the unknown number 7429-?=4358-1587
Solution:
- Take the unknown value as [latex]x[/latex]
by substituting [latex]x[/latex],
7429 - [latex]x[/latex] = 4358 - 1587
7429 - [latex]x[/latex] = 2771
[latex]x[/latex] = 7429 - 2771
[latex]x[/latex] = 4658
Therefore, the unknown value [latex]x[/latex] = 4658
- As, Face value is the value of digit itself and should relate place with 'place value'
Given digit is 38745962
Therefore, face value of 7 is 7
(100 is multiplied since 9 is in hundred's place)
Place value of 9 is (9 × 100)=900
- Given that Dividend = 132, Quotient = 12, Remainder = 0
[Divisor × Quotient] + Remainder=Dividend
by substituting the given values,
[Divisor × 12] + 0 = 132
Divisor = [latex]\frac{132}{12}[/latex]
∴ Divisor = 11
- Given product is (234 × 256 × 457 × 952)
Here units digits are 4,6,7,2
Therefore, product of Units digit in the given product = 4 × 6 × 7 × 2 = 336.
- a)19
b)11
c) 16
d) 13
- As Prime number is the number which has exactly two factors namely itself
Factors of 19 = 1, 19
Factors of 11 = 1, 11
Factors of 16 = 1, 2, 4, 16
Factors of 13 = 1, 13
Therefore, 16 is not a prime as it is divisible by more than twice numbers.
- Given digit is 23679715
(Sum of digits at odd places) - (Sum of digits at even places)
Digits at odd places = 5, 7, 7, 3
Digits at even places = 1, 9, 6, 2
⇒ (5 + 7 + 7 + 3) - (1 + 9 + 6 + 2)
⇒ 22 - 18 = 4
as 4 is not divisible by 11, 23679715 also not divisible by 11