Simplification:
Directions for Questions (1 – 10): What value should come in place of the question marks (?) in the following questions?
1. (13056 ÷ 32)(513 ÷ 19) = ? + 95 [latex] \sqrt{1104 + 40 × 30} [/latex]

A. 6456 B. 6455 C. 6457 D. 6454 E. 6458

Answer: Option A
Solution: (13056 ÷ 32)(513 ÷ 19) = ? + 95 [latex] \sqrt{1104 + 40 × 30} [/latex]
408 x 27 = ? + 95 [latex] \sqrt{1104 + 200} [/latex]
11016 = ? + 95 [latex] \sqrt{2304} [/latex]
? = 11016 - 95 x 48
? = 11016 - 4560
? = 6456
2. [latex] \sqrt{29 × 1240 ÷ 31 + 173 × 5} [/latex] × 36 =[latex] ?^2 [/latex] + 29 × 16

A. 32 B. 33 C. 35 D. 31 E. 34

Answer: Option E
Solution: [latex] \sqrt{29 × 1240 ÷ 31 + 173 × 5} [/latex] × 36 =[latex] ?^2 [/latex] + 29 × 16
[latex] \sqrt{29 × 40 + 865} [/latex] × 36 = [latex] ?^2 [/latex] + 464
[latex] \sqrt{1160 + 865} [/latex] × 36 = [latex] ?^2 [/latex] + 464
[latex] ?^2 [/latex] = 45 x 36 - 464
[latex] ?^2 [/latex] = 1620 - 464
[latex] ?^2 [/latex] = 1156
[latex] ?^2 [/latex] = [latex] \sqrt {1156}[/latex]
[latex] ?^2 [/latex] = 34
3. (16980 - 9910 - 4648) ÷ 14 = ? + (16650 ÷ 111)

A. 23 B. 21 C. 22 D. 24 E. 25

Answer: Option A
Solution: (16980 - 9910 - 4648) ÷ 14 = ? + (16650 ÷ 111)
(16980 - 14558) ÷ 14 ? + 150
2422 ÷ 14 ? + 150
? + 150 = 173
? = 173 - 150 = 23
4. 73% of 4936 + 24% of 5612 - 55% of 3848 = ?

A. 2833.76 B. 2831.56 C. 2832.12 D. 2834.54 E. 2835.45

Answer: Option A
Solution: 73% of 4936 + 24% of 5612 - 55% of 3848 = ?
[latex] \frac{73} {100}[/latex] x 4936 + [latex] \frac{24} {100}[/latex] x 5612 - [latex] \frac{55} {100} [/latex] x 3848
? = 73 x 49.36 + 24 x 56.12 - 55 x 38.48
? = 3603.28 + 1346.88 - 2116.4
? = 4950.16 - 2116.4 = 2833.76
5. [latex] \frac{8} {13}[/latex] - [latex] \frac{7} {26}[/latex] x [latex] ?^2 [/latex] = 234

A. 25 B. 26 C. 27 D. 24 E. 23

Answer: Option B
Solution: [latex] \frac{8} {13}[/latex] - [latex] \frac{7} {26}[/latex] x [latex] ?^2 [/latex] = 234
[latex] \frac{16 − 7} {26}[/latex] [latex] ?^2 [/latex] = 234
[latex] \frac{9} {26}[/latex][latex] ?^2 [/latex] = 234
[latex] ?^2 [/latex] = 676
? = [latex] \sqrt{676}[/latex]= 26

Simplification:
Directions for Questions (1 – 5): What approximate value should come in place of the question mark (?) in the following questions? (Note : You are not expected to calculate the exact value)
1. 32% of 1699.98 + 71.93% of 225.10 = ? + 19% of 1101

A. 498 B. 499 C. 497 D. 500 E. 496

Answer: Option C
Solution: (32% of 1699.98 + 71.93% of 225.10 = ? + 19% of 1101
[latex] \frac{32} {100} [/latex] x [latex] \frac{72} {100} [/latex]x 225 ≈ ? + [latex] \frac{19} {100}[/latex] x 1101
? + 19 x 11.01 = 32 x 17 + 9 x 18
? + 209 ≈ 544 + 162
? = 706 - 209 = 497
2. 27.04 x 116.95 ÷ 12.98 + [latex] (87.01)^2 [/latex] = ? + 7312

A. 501 B. 500 C. 502 D. 499 E. 503

Answer: Option B
Solution: 27.04 x 116.95 ÷ 12.98 + [latex] (87.01)^2 [/latex] = ? + 7312
27 x 117 ÷ 13 + [latex] (87.01)^2 [/latex] = ? + 7312
? + 7312 = 27 x 9 + 7569
? + 7312 = 27 x 9 + 7569
? = 257 + 243
? = 500
3. [latex] \frac{1} {43} [/latex] of 4817 + (82.01 x 21) = ? + (37272 ÷ 24.02)

A. 285 B. 286 C. 284 D. 281 E. 278

Answer: Option D
Solution: [latex] \frac{1} {43} [/latex] of 4817 + (82.01 x 21) = ? + (37272 ÷ 24.02)
[latex] \frac{1} {43} [/latex] 4817 + (82 x 21) ≈ ? + (37272 ÷ 24)
? + 150
? + 1553 = 112. 02 + 1722
? ≈ 169 + 112
? = 281
4. 48% of 6410 + 71% of 8108 = ? [latex] - (45.02)^2 [/latex]

A. 10848 B. 10849 C. 10847 D. 10846 E. 10845

Answer: Option A
Solution: 48% of 6410 + 71% of 8108 = ? [latex] - (45.02)^2 [/latex]
[latex] \frac{48} {100}[/latex] x 6410 + [latex] \frac{24} {100}[/latex] x 8108 ≈ ? [latex] - (45)^2 [/latex]
- 2025 = 48 x 64.10 + 71 x 81.08
- 2025 ≈ 3072 + 5751
? = 8823 + 2025
? = 10848
5. 27.01 of [latex] \frac{5} {81}[/latex] of 8700 + [latex] \sqrt{27.02 × 19 + 9 × 24} [/latex] = [latex] ?^2 [/latex] - 24

A. 13 B. 12 C. 14 D. 15 E. 11

Answer: Option C
Solution: 27.01 of [latex] \frac{5} {81}[/latex] of 8700 + [latex] \sqrt{27.02 × 19 + 9 × 24} [/latex] = [latex] ?^2 [/latex] - 24
[latex] \frac{27} {100}[/latex] [latex]\frac{5} {81} [/latex] x 8700 + [latex] \sqrt{27 × 19 + 9 × 24} [/latex] = [latex] ?^2 [/latex] - 24
[latex] ?^2 [/latex] - 24 = 5 x 29 + [latex] \sqrt{513 + 216} [/latex]
[latex] ?^2 [/latex] - 24 = 145 + [latex] \sqrt{729} [/latex]
[latex] ?^2 [/latex] = 145 + 27 + 24 = 196
[latex] ?^2 [/latex] = [latex] \sqrt{196} [/latex]
= 14
Number Series:

Mensuration:
1. The breadth of a rectangle is equal to the diameter of a circle. The circumference of a circle is equal to the perimeter of a square of side 33m. What is the length of a rectangle. If the area of a rectangle is 756[latex] m^2 [/latex]?

A. 18m B. 19m C. 20m D. 17m E. 16m

Answer: Option A
Solution: According to the question,
Perimeter of a square = 4 × side
Perimeter of a square = 4 × 33 = 132m
Circumference of a circle 2πr
132 = 2 [latex] \frac{22} {7}[/latex] × r
r = 21m
Diameter of a circle = 2r
Diameter of a circle = 2 × 21 = 42m
Breadth of a rectangle = 42m
Area of a rectangle = 756 [latex] m^2 [/latex]
Area of a rectangle = Length of a rectangle × Breadth of a rectangle
Length of a rectangle = [latex] \frac{756} {42}[/latex] = 18m
Compound Interest:
2. What will be the compound interest on a sum of Rs. 44,375 at compound interest compounded annually at 12% per annum in two years?

A. Rs.11,288 B. Rs.11,290 C. Rs.11,289 D. Rs.11,287 E. Rs.11,291

Answer: Option C
Solution: According to the question,
P = Rs.44,375
r = 12%
t = 2 years
C.I = P({1 + [latex] \frac{r} {100})^t[/latex] - 1}
C.I = 44375{(1 + [latex] \frac{12} {100})^2[/latex]- 1}
C.I = 44375{( [latex] \frac{25 + 3} {25})^2[/latex]- 1}
C.I = 44375{[latex] \frac{784 } {625}[/latex] - 1}
C.I = 44375{[latex] \frac{784 - 625} {625}[/latex]}
C.I = 44375 x [latex] \frac{159} {625}[/latex]
C.I = 71 x 159 = Rs.11,289
Time and work:
3. 14 girls and 10 boys can do a piece of work in 5 days while 14 girls and 6 boys can do the same piece of work in 6 days. In how many days can 19 girls and 16 boys do the same piece of work?

A. 3[latex] \frac{6} {7}[/latex] days B. 3[latex] \frac{5} {7}[/latex] days C. 3[latex] \frac{2} {7}[/latex] days D. 3[latex] \frac{3} {7}[/latex] days E. 3[latex] \frac{4} {7}[/latex] days

Answer: Option D
Solution: 14 girls and 10 boys 1 day work
14 girls and 6 boys 1 day work
According to the question,
(14 girls + 10 boys) × 5 ≡ (14 girls + 6 boys) × 6
(70 girls + 50 boys) × 5 ≡ (84 girls + 36 boys) × 6
14 boys ≡ 14 girls
1 boy ≡ 1 girl
(19 girls + 50 boys) ≡ (19 girls + 16 boys) = 35 boys
M₁ D₁ = M₂ D₂
24 x 5 = 35 D₂
D₂ = [latex] \frac{5 × 24} {35}[/latex]
D₂ = 3[latex] \frac{3} {7}[/latex]
Percentage:
4. If the numerator of a fraction is increased by and denominator is also increased by then the value of fraction is [latex] \frac{4} {7}[/latex]. The original fraction is:

A. [latex] \frac{29} {50}[/latex] B. [latex] \frac{30} {55}[/latex] C. [latex] \frac{34} {55}[/latex] D. [latex] \frac{31} {55}[/latex] E. [latex] \frac{32} {55}[/latex]

Answer: Option A
Solution: According to the question,
Let the original fraction be [latex] \frac{100 x} {100 y}[/latex] then,
([latex] \frac{100 + 450} {100 + 300}[/latex])[latex] \frac{x} {y}[/latex] = [latex] \frac{4} {5}[/latex]
The original fraction
([latex] \frac{550} {400}[/latex])[latex] \frac{x} {y}[/latex] = [latex] \frac{4} {5}[/latex]
([latex] \frac{x} {y}[/latex]) = [latex] \frac{4 × 8} {11 × 5 }[/latex]
([latex] \frac{x} {y}[/latex]) = [latex] \frac{32} {55}[/latex]
The original fraction = [latex] \frac{32} {55}[/latex]
Ratio and Proportion:
5. In a college the students in Math and Hindi classes are in the ratio 17:19. When 12 more students join Hindi class the ratio becomes 17:21. How many students are there in the Hindi class?

A. 115 B. 110 C. 112 D. 114 E. 113

Answer: Option D
Solution: Let the number of students in Math and Hindi be , then According
to the question,
([latex] \frac{17 x} {19 x + 12}[/latex]) = [latex] \frac{17} {21}[/latex]
357x = 323x + 204
357x - 323x - 204
34x = 204
x = 6
Number of students in Hindi class = 19x = 19 × 6 =114
Pipes and Cistern:

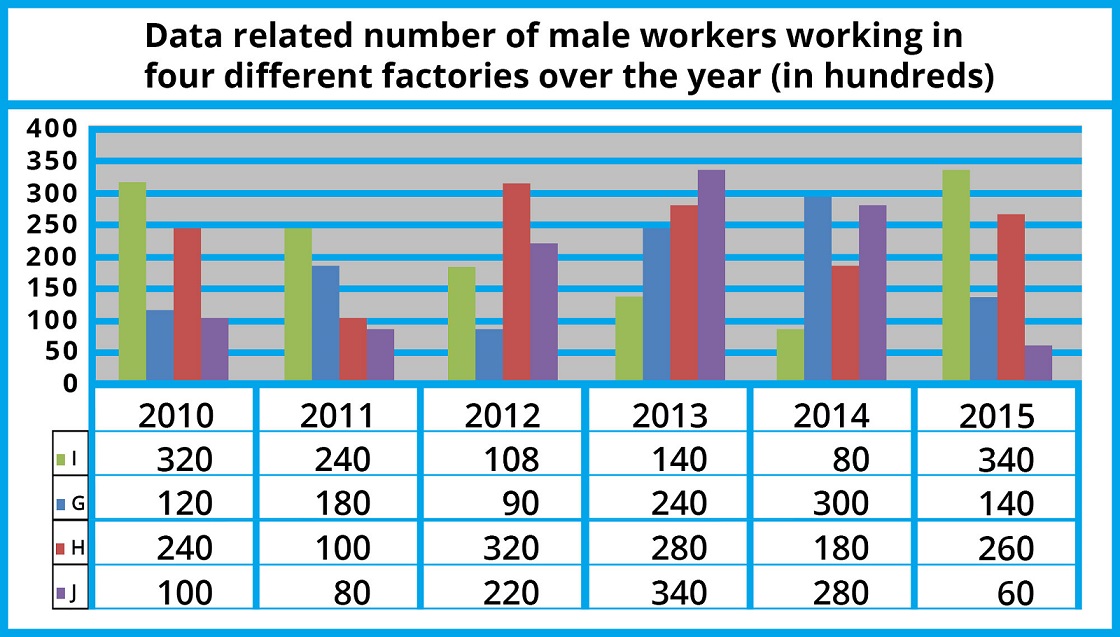
Data Interpretation:
Directions for Questions (1 - 5) Study the following line-chart carefully to answer the given questions.

1. What is the percentage increase number of male workers working in factory G in 2011 as compared to the previous year?

A. 52% B. 48% C. 55% D. 50% E. 45%

Answer: Option D
Solution: Number of male workers working in factory G in 2011
= 180 x 100 = 18000
Number of male workers working in factory G in 2010
120 x 100 = 12000
Percentage increase = [latex] \frac{18000 - 12000} {12000} [/latex] x 100
= [latex] \frac{6000} {12000} [/latex] x 100
= 50%
2. Number of male workers working in factory H in 2014 and 2015 together are approximately what percent of number of male workers working in factory I in 2010 and 2015 together?

A. 71% B. 67% C. 74% D. 64% E. 62%

Answer: Option B
Solution: Number of male workers working in factory H in 2014 and 2015 together
(180 + 260) x 100 = 44000
Number of male workers working in factory I in 2010 and 2015 together
(320 + 340) x 100 = 44000
Percentage = [latex] \frac{44000} {66000} [/latex] x 100
= [latex] \frac{4400} {6600} [/latex]
= 66.7% ≈ 67%
3. What is the difference between number of male workers working in factory I in 2010, 2011, 2012, 2013 and 2015 together and number of male workers working in factory G, H, I and J together in 2013?

A. 22120 B. 22080 C. 22050 D. 22100 E. 22000

Answer: Option E
Solution: Number of male workers working in factory I in 2010, 2011, 2012, 2013 and 2015 together
= (320 + 240 + 180 + 140 + 340) x 100
= 12200
= Number of male workers working in factory G, H, I and J together in 2013
= (240 + 180 + 140 + 340) x 100
= 10000
Difference = 12200 - 10000
= 22000
4. What is the percentage decrease in number of male workers working in factory H in 2013 as compared to the previous year?

A. 17.6% B. 15.5% C. 10.3% D. 12.5% E. 14.2%

Answer: Option D
Solution: Number of male workers working in factory H in 2013
280 X 100 = 28000
Number of male workers working in factory H in 2012
320 X 100 = 32000
Percentage decrease = [latex] \frac{32000 - 28000} {32000} [/latex] x 100
= [latex] \frac{4000} {32000} [/latex] x 100
= [latex] \frac{100} {8} [/latex]
= 12.5%
5. What is the ratio between number of male workers working in factory G and J together in 2014 to number of male workers working in factory H and I together in 2015?

A. 29 : 30 B. 19 : 20 C. 29 : 20 D. 30 : 19 E. 30 : 29

Answer: Option A
Solution: Number of male workers working in factory G and J together in 2014
Number of male workers working in factory G and J together in 2014
= (300 + 280) x 100
= 58000
Number of male workers working in factory H and I together in 2015
= (260 + 340 x 100
= 60000
Ratio = [latex] \frac{58000} {60000} [/latex]
= [latex] \frac{58} {60} [/latex]
= 29 : 30

1. Prime factors of 40 are _______.

1. 2 x 2 x 3 x 5 x 5
2. 2 x 3 x 5 x 5
3. 2 x 2 x 2 x 5
4. 2 x 3 x 5

Correct Answer: 3 2. Answer of following (a³b)⁴is ________.

1. a¹⁴b⁵
2. a⁸b⁴
3. a¹²b⁴
4. a¹⁰b³

Correct Answer: 3 3. Tan(α + β) = ___________.

1. tanα-tanβ/1 + tanαtanβ
2. tanα+tanβ/1 - tanαtanβ
3. cotα+cotβ/1-cotαcotβ
4. cotα-cotβ/1 + cotαcotβ

Correct Answer: 2 4. Path described by any moving point is classified as ___________.

1. ordinate ray rays
2. line segment
3. rays
4. line

Correct Answer: 4 5. The sector of a circle has radius of 21 cm and central angle 135o. Find its perimeter?

1. 91.5 cm
2. 93.5 cm
3. 94.5 cm
4. 92.5 cm

Correct Answer: 1 Solution: Perimeter of the sector = length of the arc + 2(radius) = (135/360 * 2 * 22/7 * 21) + 2(21) = 49.5 + 42 = 91.5 cm 6. The middle value of an ordered array of numbers is the

1. Mode
2. Mean
3. Median
4. MidPoint

Correct Answer: 3 7. Which of the following is not a measure of central tendency?

1. Percentile
2. Quartile
3. Standard deviation
4. Mode

Correct Answer: 3 Solution: Standard Deviation is measure of Dispersion or variability its not measure of central tendency. 8. What will be the cost of building a fence around a square plot with area equal to 289 sq ft, if the price per foot of building the fence is Rs. 58?

1. Rs. 3944
2. Rs. 3828
3. Rs. 4176
4. Cannot be determined

Correct Answer: 1 Solution: Let the side of the square plot be a ft. a² = 289 => a = 17 Length of the fence = Perimeter of the plot = 4a = 68 ft. Cost of building the fence = 68 * 58 = Rs. 3944. 9. In a triangle ABC, if angle A = 72° , angle B = 48° and c = 9 cm then Ĉ is

1. 69°
2. 66°
3. 60°
4. 63°

Correct Answer: 3 10. In a chess tournament each of six players will play every other player exactly once. How many matches will be played during the tournament?

1. 12
2. 15
3. 30
4. 36

Correct Answer: 2 Solution:

1. matches of first player with other 5 players
2. matches of second player with 4 players other than the first player

III. matches of third player with 3 players other than the first player and second player.

1. matches of fourth player with 2 players other than the first player, second player and third player.
2. matches of fifth player with 1 player other than the first player, second player, third player and fourth player.

So total matches will be 5+4+3+2+1 = 15