Directions[1-2]: In the following question, two equations numbered I and II are given. You have to solve both the equations and give answer:
1. I. [latex]2{X}^{2} + 21 = 17X[/latex] II. [latex]{Y}^{2} + \sqrt{3136} = 15Y[/latex]

A. If X > Y B. if Y < X C. If X ≥ Y D. If Y ≥ X

Answer - Option D
Explanation - I. [latex]2{X}^{2} + 21 = 17X[/latex]
II. [latex]{y}^{2} + \sqrt{3136} = 15Y[/latex]
I. [latex]2{X}^{2} + 21 = 17X[/latex]
(X – 7)(2X – 3) = 0
⇒ X = +7, + [latex]\frac {3}{2}[/latex]
II. [latex]{y}^{2} + \sqrt{3136} = 15Y[/latex]
II. [latex]{y}^{2} + 56 - 15Y = 0[/latex]
(Y – 7)(Y – 8) = 0
⇒ Y = +7, +8
Y ≥ X
2. I. [latex]12{X}^{2} + 11X + 2 = 0[/latex] II. [latex]12{Y}^{2} + 7Y + 1 = 0[/latex]

A. X > Y B. X ≥ Y C. X < Y D. X = Y or the relationship cannot be established

Answer - Option D
Explanation - X= [latex]\frac {-2}{3}, \frac {-1}{4}[/latex]
Y= [latex]\frac {-1}{3}, \frac {-1}{4}[/latex]
Directions[3-5]: What should come in place of question mark (?) in the following number series?
3. 705, 728, 774, 843, 935, 1050, ?

A. 1190 B. 1180 C. 1185 D. 1188

Answer - Option D
Explanation - 705 + 23 × 1 = 728
728 + 23 × 2 = 774
774 + 23 × 3 = 843
843 + 23 × 4 = 935
935 + 23 × 5 = 1050
1050 + 23 × 6 = 1188
4. 499, 622, 868, 1237, 1729, 2344, ?

A. 3205 B. 3082 C. 2959 D. 3462

Answer - Option B
Explanation - 499 + 1 × 123 = 622;
622 + 2 × 123 = 868
868 + 3 × 123 = 1237;
1237 + 4 × 123 = 1729
1729 + 5 × 123 = 2344;
2344 + 6 × 123 = 3082
5. 14, 15, 23, 32, 96, ?

A. 111 B. 124 C. 152 D. 121

Answer - Option D
Explanation - [latex]14 + {1}^{2} = 15; 15 + {2}^{3} = 23[/latex]
[latex]23 + {3}^{2} = 32; 32 + {4}^{3} = 96[/latex]
[latex]96 + {5}^{2} = 121[/latex]
Since difference is alternating square and cube of increasing numbers

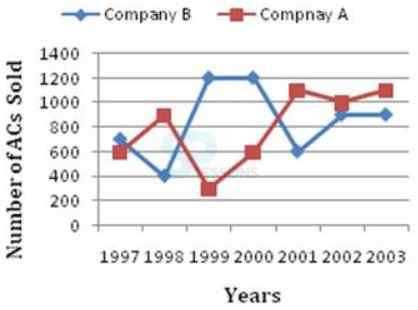
Directions[1-5]: Study the following graph carefully to answer the questions that follow:

Number of ACs sold by two companies A and B over the years.

1. Sales in the year 2001 for Company A forms what per cent of total sales of Company A for all the years together? (rounded off to two decimal points)

A. 19.64 B. 12.30 C. 24.46 D. 29.19

Answer - Option A
Explanation - Required percentage = [latex]\frac {1100 \times 100}{5600}[/latex] =19.64
2. Which of the following combinations of year and percentage rise in sales with respect to previous year for Company A is correct? (Percentage rounded off to two decimal points)

A. 2000—89.85 B. 2001—83.33 C. 1998—43.21 D. 2003—7.68

Answer - Option B
Explanation - Percentage rise for the year 2001 is given as:
=[latex] \frac {(Number of ACs sold in 2001 - Number of ACs sold on 2000)}{(Number of ACs sold on 2000)} \times 100[/latex]
= [latex] \frac {(1100-600)}{600} \times 100[/latex]
= [latex] \frac {500}{600} \times 100[/latex]
=83.33
Similarly calculating the percentage rise for respective years in the options given, we would see that the correct combination is for the only year 2001,
The correct combinations should be 2001
= 83.33
3. Total sales of Company B for the years 1997, 1998 and 2001 together is what per cent of the total sales of Company B for all the years together? (rounded off to two decimal points).

A. 24.37 B. 35.64 C. 28.81 D. 37.29

Answer - Option C
Explanation - The required percentage = [latex] \frac {(700 + 400 + 600)}{5900} \times 100 = \frac {1700}{59}[/latex] ≈ 28.81
4. What is the ratio of total sales of Company A to the total sales of Company B over the years?

A. 26:29 B. 27:31 C. 53:51 D. 56:59

Answer - Option D
Explanation - The required ratio=5600:5900=56:59
5. During which year was percentage rise/fall in sales from the previous year the highest for Company A?

A. 1999 B. 2001 C. 1998 D. 2000

Answer - Option D
Explanation - The increase was 100% from 1999 to 2000, and 83% from 2000 to 2001 even though the absolute growth was higher in 2001, the growth in percentage was higher for 2000.

1. A started business with Rs. 32000 and B joined him after certain number of months with a capital of Rs. 36000. At the end of a year, the profit is divided in the ratio of 4: 3. When did B join?

A. 5 months B. 7 months C. 9 months D. 4 months

Answer - Option D
Explanation - The ratio of share of A and B = [latex][(32000 \times 12): (36000 \times x)][/latex]
The profits divided in the ratio of 4: 3,
According to the question,
[latex]\frac {(32000 \times 12)}{(36000 \times x)} = \frac {4}{3}[/latex]
[latex]\frac {(8 \times 12)}{(9x)} = \frac {4}{3}[/latex]
X = 8 months
B joined after 4 months.
2. If the compound interest on a certain sum for 2 years at 5% per annum is Rs. 2050, then find the corresponding simple interest?

A. 1950 B. 2000 C. 1970 D. 1930

Answer - Option B
3. 30 men can complete the work on 15 days and 5 men left after 8 days. Some women were replaced to complete the remaining work. If work should be completed in agreed time, then how many women were being replaced?

A. 5 women B. 7 women C. 8 women D. 4 women

Answer - Option A
Explanation - Total work = men [latex]\times[/latex] days
Total work = 30 [latex]\times[/latex] 15 = 450
8 days work = 30 [latex]\times[/latex] 8 = 240
Remaining work = 450 – 240 = 210
Let the number of women replaced be x,
[latex]\frac {210}{(25 + x)}[/latex] = 7
25 + x = 30
X = 5 women
4. A boat can travel 44 km downstream in 66 min. The ratio of the speed of the boat in still water to the speed of the stream is 3: 1. How much time will the boat take to cover 75 km upstream?

A. 3 hour 15 min B. 2 hour 25 min C. 3 hour 45 min D. 4 hour 30 min

Answer - Option C
Explanation - Speed of downstream = [latex] \frac {D}{T} = \frac {44}{(\frac {66}{60})} = 44 \times (\frac {60}{66}) = 40[/latex] km/hr
The ratio of the speed of the boat in still water to the speed of the stream
[latex]\Rightarrow[/latex] 3 : 1 (3x, x)
4x = 40
X = 10
Speed of upstream = 3x – x = 2x = 20 km/hr
Distance = 75 km
Time = [latex]\frac {D}{S} = \frac {75}{20} = 3 \frac {3}{4}[/latex] hr = 3 hour 45 min
5. The ratio between the ages of two persons A and B is 3: 5. The difference between their ages is 12 years. Find the age of another person C if the average age of all the persons, after 4 years will be 27 years?

A. 21 years B. 19 years C. 17 years D. 23 years

Answer - Option A
Explanation - The ratio between the ages of two persons A and B = 3: 5 (3x, 5x)
5x – 3x = 12
2x = 12
X = 6 years
A’s present age = 6 [latex]\times[/latex] 3 = 18 years
B’s present age = 6 [latex]\times[/latex] 5 = 30 years
Total present ages of A, B and C = (27 [latex]\times[/latex] 3) – 12 = 69 years
Present age of C = 69 – (18 + 30) = 21 years