Introduction
Introduction
Data Interpretation is the ability to analyze, interpret and visualize the provided data to arrive at conclusions and to make inferences. Data Interpretation questions in the competitive exams is a test of analytical abilities. In the competitive exams, the Data Interpretation questions are grouped together and refer to the same table, graph or other data/visual presentation. The test takers are required to interpret or analyze the given data to answer the questions. In India, competitive exams related to employment in Banking, SSC, Insurance etc..have the Data Interpretation type of questions.
 Practice Sets
Practice Sets
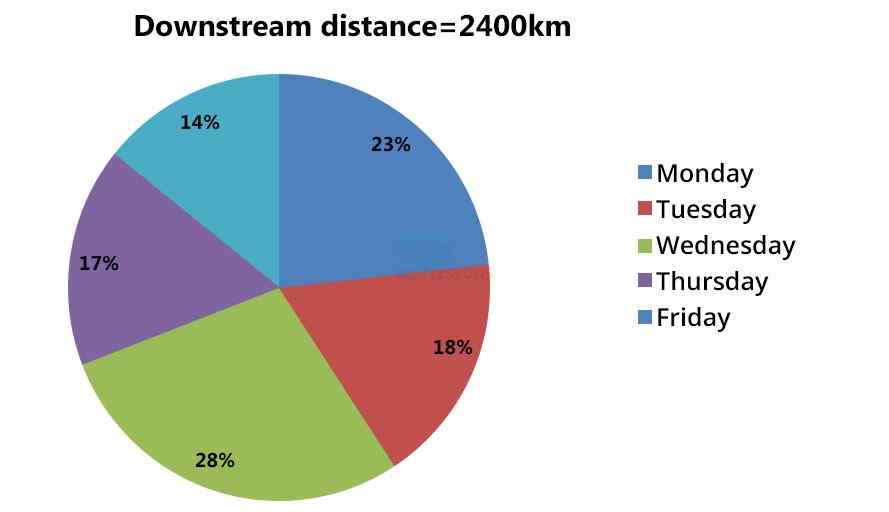
Direction (1-5): Study the data given below and answer the following question. The pie charts shown below shows the distance covered by a boat moving upstream and downstream in different days of a week. And the table shows the speed of stream in km/hr. in different days of a week.
The table shows the speed of the stream in different days in the week and some data are missing.
1) If the time taken by boat to travel upstream on Friday is equal to the time taken by it to travel downstream on Monday and the speed of boat in still water on Monday is 15 kmph then find the speed of boat in still water on Friday?
(252)/(b - 4) = (552)/(15 + 8)
2(b - 4) = 21
b = 14.5kmph
2) If the speed of boat in still water on Tuesday was 10kmph and the speed of boat in still water on Wednesday was 80% of Tuesday and time taken to travel downstream on Tuesday is 18 hrs more than the time taken by it to travel upstream on Wednesday, then find the speed of stream on Tuesday?
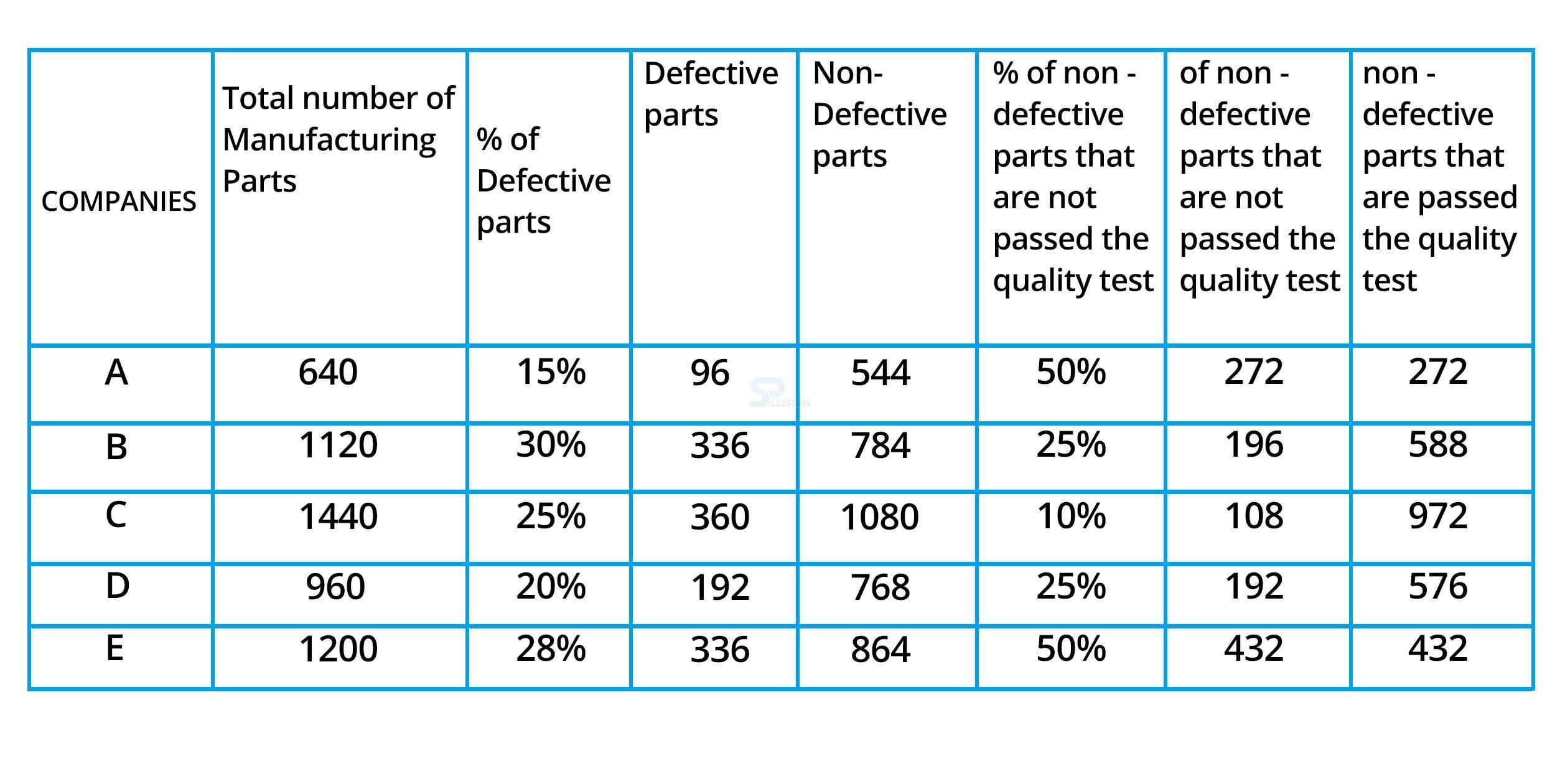
11) If both the years the percentage of defective parts from company D is equal, and in 2017 only 10% of nondefective parts are not passed the quality test for company D, then what is the total number of non-defective parts that are passed the quality test in both years from company D?
The total number of Non-defective parts that are passed from quality test from company C and D in 2016 = 972 + 576
= 1548
Total number of Non-defective parts from A, B and E together in 2017 = 768 + 960 + 850 = 2578
Required percentage = [(2578 – 1548) /2578] * 100 = 39.99% = 40% less
14) What is the average number of non-defective parts that are not passed the quality test from all the company except D in 2016?
Note:
Saturday and Sunday are holidays
“-“ is missing value, we have to find the value according to the question.
16) Find the ratio of the number of lectures taken by A to that of the number of lectures taken by D in a week?
| Day | Speed of stream |
|---|---|
| Monday | 8 |
| Tuesday | - |
| Wednesday | 12 |
| Thursday | - |
| Friday | 4 |
- a) 14.5kmph
b) 15kmph
c) 16.5kmph
d) 12kmph
e) None of these
| Day | Upstream distance | Downstream distance | Speed of stream |
|---|---|---|---|
| Monday | 576 | 552 | 8 |
| Tuesday | 324 | 432 | - |
| Wednesday | 360 | 672 | 12 |
| Thursday | 288 | 408 | - |
| Friday | 252 | 336 | - |
- a) 2kmph
b) 6kmph
c) 4kmph
d) 8kmph
e) None of these
- a) 15(3/7) kmph
b) 18(3/7) kmph
c) 12(3/7) kmph
d) 11(3/7) kmph
e) None of these
- a) 12 hours
b) 16 hours
c) 25 hours
d) 24 hours
e) 18 hours
- a) 3(11/29) kmph
b) 2(11/29) kmph
c) 4(12/19) kmph
d) 5(13/19) kmph
e) None of these
Solution Explantion:
Scheme Q: The Total Number of Projects under Scheme Q = 375
The Number of Projects in City B is 75 less than that of number of projects in City A and C together.
Consider the number of projects in City A and C is X, then X + (X – 75) = 375, on solving we get, X = 225, then number of projects in City B = 150 projects.
Scheme P: The Number of Projects in City B is 2/3rd of the Number of projects in city B under Scheme Q.
Scheme P: Number of Projects in City B = 2/3rd * 150 = 100 projects.
Scheme Q: The Number of Projects in City A is 5/6th of the number of projects in City A under Scheme R.
Scheme R: The Number of Projects under Scheme R is 4/5th of the number of Projects under Scheme Q.
Therefore, the total number of projects in Scheme R is 300.
The Number of Projects in City A is equal to the number of Projects in City B under Scheme Q.
Therefore number of projects in city A under scheme R is 150 projects.
Scheme R: The Number of Projects in city C under Scheme Q and Scheme R is Equal. So there are 100 projects in city C under scheme R. And also for city B under scheme R should have 50 projects.
Scheme P: The Number of Projects in City C is 4/5th of the Number of projects in city C under Scheme R. Number of Projects in City C= 4/5 * 100 = 80
The Total Number of Projects in city A and City C is equal under Scheme P.
Therefore number of projects in City A is 80 projects. So the final table becomes
6) In 2019, the projects allocated for city B under Scheme Q is increases by 30%, and the project allocated for city C under scheme R is decreases by 45%, then the total number of projects in 2019 for city B under scheme Q and City C under Scheme R is equal to total number of projects in which of the following Cities in 2018?
| City/Schemes | Scheme P | Scheme Q | Scheme R |
|---|---|---|---|
| City A | 80 | 125 | 150 |
| City B | 100 | 150 | 50 |
| City C | 80 | 100 | 100 |
| Total | 260 | 375 | 300 |
| City/Schemes | Scheme P | Scheme Q | Scheme R |
|---|---|---|---|
| City A | |||
| City B | 100 | 150 | |
| City C | |||
| Total | 375 |
| City/Schemes | Scheme P | Scheme Q | Scheme R |
|---|---|---|---|
| City A | [latex](\frac{5}{6})^th[/latex] | ||
| City B | 100 | 150 | |
| City C | |||
| Total | 375 |
| City/Schemes | Scheme P | Scheme Q | Scheme R |
|---|---|---|---|
| City A | 125 | 150 | |
| City B | 100 | 150 | |
| City C | 100 | ||
| Total | 375 | 300 |
| City/Schemes | Scheme P | Scheme Q | Scheme R |
|---|---|---|---|
| City A | 80 | 125 | 150 |
| City B | 100 | 150 | 50 |
| City C | 80 | 100 | 100 |
| Total | 260 | 375 | 300 |
- a) City C under Scheme P and City A under scheme R together
b) City B under Scheme P and City C under scheme P together
c) City A under Scheme Q and City B under scheme R together
d) City C under Scheme Q and City A under scheme R together
e) None of those given as options
- a) 75
b) 80
c) 100
d) 150
e) None of those given as option
- a) 48000
b) 3800
c) 4800
d) 54000
e) None of those given as option
- a) 560
b) 675
c) 720
d) None of those given as option
e) 635
- a) 154
b) 100
c) 94
d) 114
e) None of those given as option
| COMPANIES | % of Defective parts | % of non- defective parts that are not passed the quality test |
|---|---|---|
| A | 15% | 50% |
| B | 30% | 25% |
| C | 25% | 10% |
| D | 20% | 25% |
| E | 28% | 50% |
- a) 1656
b) 306
c) 1556
d) 1666
e) None of those given as option
- a) 3: 7
b) 53: 52
c) 4 : 9
d) 19 : 17
e) Cannot be determined
- a) 38% More
b) 50% less
c) 28 % More
d) 40% less
e) None of those given as option
| COMPANIES | Total number of Manufacturing Parts | % of Defective parts | Defective parts | Non- Defective parts |
|---|---|---|---|---|
| A | 960 | 20% | 192 | 768 |
| B | 1280 | 25% | 320 | 960 |
| E | 1000 | 15% | 150 | 850 |
- a) 254
b) 248
c) 220
d) None of those given as option
e) 252
- a) 664
b) 786
c) 544
d) 684
e) None of those given as option
| Tutors | Number of classes taken on Monday, Tuesday and Wednesday by each | Number of classes taken on Thursday and Friday by each | Salary per class (In Rs.) |
|---|---|---|---|
| A | 2 | 0 | 5000 |
| B | 3 | - | 8000 |
| C | 1 | 3 | 6000 |
| D | 2 | 2 | 4000 |
- a) 3 : 5
b) 4 : 7
c) 5 : 9
d) 11 : 13
e) None of these
- a) Rs. 306000
b) Rs. 282000
c) Rs. 348000
d) Rs. 324000
e) None of these
- a) Rs. 74000
b) Rs. 66000
c) Rs. 82000
d) Rs. 70000
e) None of these
- a) Rs. 116000
b) Rs. 104000
c) Rs. 95000
d) Rs. 88000
e) None of these
- a) 2
b) 4
c) 3
d) 1
e) None of these
- a) Rs3450
b) Rs Rs3600
c) Rs4270
d) Rs3300
e) None of these
- a) Rs5814
b) Rs5678
c) Rs4678
d) Rs6234
e) None of these
- a) Rs2256
b) Rs2860
c) Rs1890
d) Rs2450
e) Rs2160
- a) Rs6420
b) Rs5360
c) Rs5440
d) Rs6640
e) None of these
- a) Rs2428
b) Rs2256
c) Rs2786
d) Rs2280
e) None of these
Directions (1-5): Follow the given instruction to give the answer of the following questions.
Total number who attended the workshop = Number of Literates + Number of illiterates
1) The total number of people (literates + illiterates) who attended the workshop on Monday was what % more than those who attended on Friday?
11) If the ratio of boys and girls in college A for civil engineering students are 4:1 and the civil engineering students are 50% more than the mechanical engineering students. Then find the difference of boys and girls in civil department?
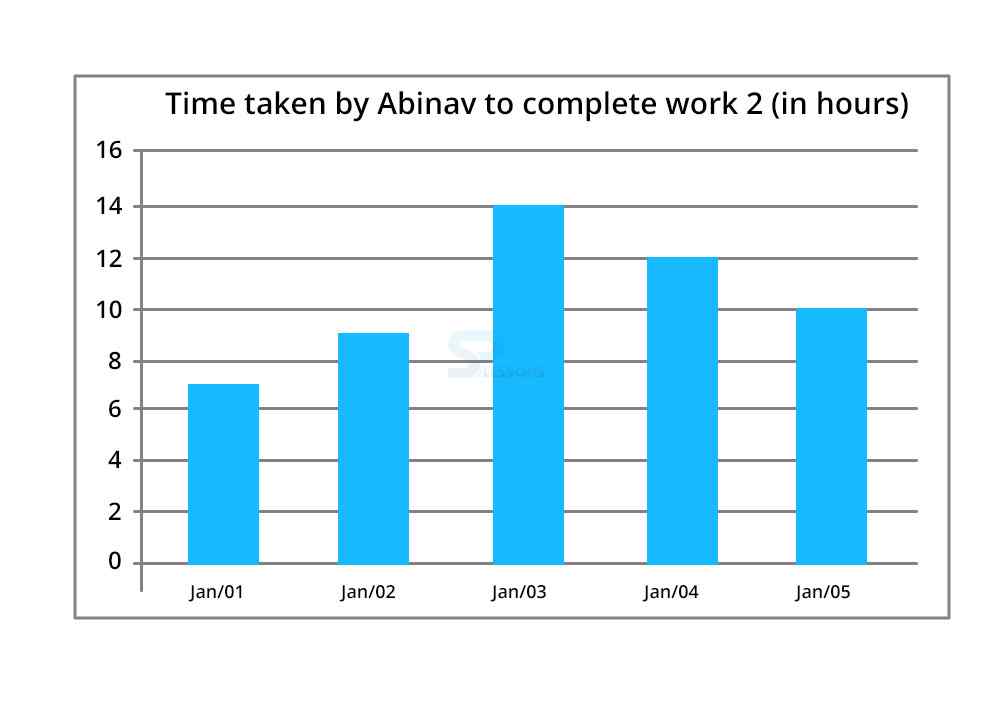
There is also the line graph which shows the time taken by Abinav to complete work 2 if it completes whole work with efficiency of different days.
Note- The ratio of efficiency of Anand to Abinav to do work 2 on different days is same as data given in the table for work 1.
16) Anand and Abinav both started to complete work 1 on Jan 2 but Anand left after working for 2 hours. Another person Ajay whose efficiency is 60% of the efficiency of Anand (as of Jan 2) joins with Abinav. Abinav leaves 2 hours before the completion of work then Ajay alone finishes the remaining work. What is the total time in which work 1 is completed.
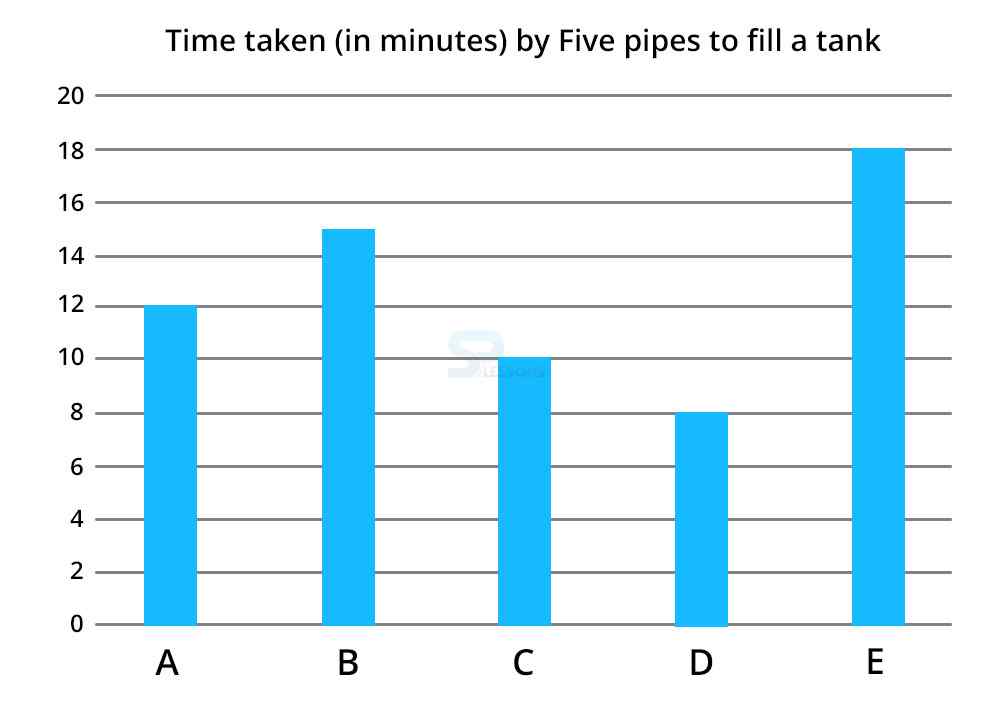
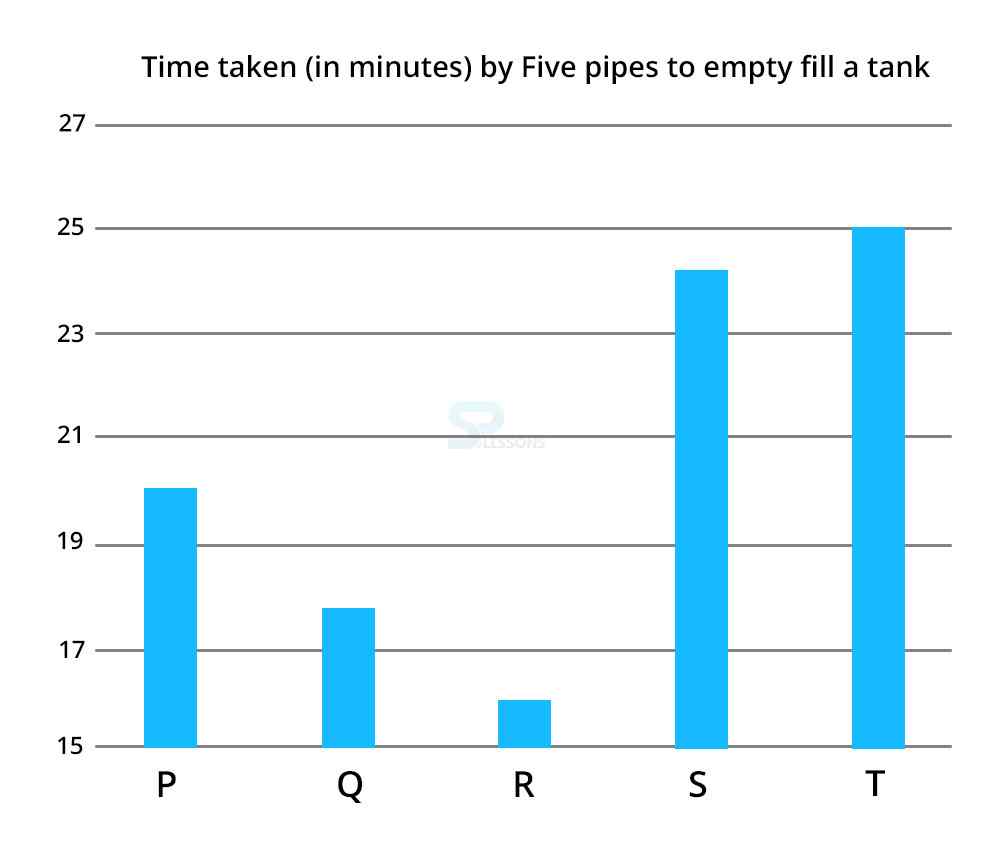
21) Pipe A and Pipe B opened simultaneously for 4 minutes, then closed and then pipe F and pipe Q are opened for 2 minutes, then closed. Find the time taken by pipe G to fill the remaining part of the tank.
| Day | No. of literates (males+ Females) | Overall ratio (illiterate : literates) (out of those who attended) | Number of males (literates + illiterates) (out of those who attended) |
|---|---|---|---|
| Monday | 420 | 5:6 | 250 |
| Tuesday | 350 | 3:5 | 240 |
| Wednesday | 320 | 5:4 | 320 |
| Thursday | 300 | 6:5 | 300 |
| Friday | 420 | 2:3 | 320 |
- a) 12%
b) 10%
c) 15%
d) 18%
e) None of these
- a) 292
b) 300
c) 275
d) 280
e) None of these
- a) 12
b) 14
c) 15
d) 18
e) None of these
- a) 390
b) 400
c) 300
d) 370
e) None of these
- a) 5:9
b) 9:7
c) 7:9
d) 1:3
e) None of these
Solution Explanation:Number of employees in production, HR and finance together in company A = (60/100) * 9000 = 5400
Number of employees in R&D (in A) = 1300
Number of employees in marketing (in A) = 1440
Number of employees in accounts (in A) = 860
The number of employees in Marketing was 20 % less than that of HR department.
So, 1440 = (100 - 20) % of HR department
Number of employees in HR (in A) = 1440 * (100/80) = 1800
We have, Production + HR + Finance = 5400
Production + 1800 + Finance = 5400
Production + Finance = 3600 .................... (1)
Let the number of employees in finance be X.
Given that the number of employees in the Production department was 25 % more than that of the finance department.
So, the number of employees in Production in A = (125/100) X
Now equation (1) becomes,
(125/100)X + X = 3600
X = 1600.
Number of employees in finance (in A) = 1600
Number of employees in production (in A) = (125/100) * 1600 = 2000
Number of employees in marketing (in B)= 900
12% of total Number of employees in B = 900
Total Number of employees in B= (100/12) * 900 = 7500
Given that, the number of employees in Marketing was 40 % less than that of HR department
So, 900 = (100 - 40)% of Number of employees in HR (in B)
Number of employees in HR (in B) = 1500
Given that, the number of employees in production from company B was 10 % less than the same department from
Company A.
So, Number of employees in Production (in B) = (100 - 10) % 0f 2000 = (90/100) * 2000 = 1800
Number of employees in accounts (in B) = 500
Also given that, the total Number of employees in finance and R&D together were double the total Number of
employees in Marketing and accounts together
So, (Finance + R&D (in B) = 2 * (Marketing + accounts)(in B)
(Finance + Finance) (in B) = 2*(900 + 500) since, finance = R&D
2 * Finance = 2 * 1400
Number of employees in Finance (in B)= 1400
Number of employees in R&D (in B)= 1400
6) What is the difference between the total Number of employees in Marketing and accounts together in Company A and that in the same courses together in Company B?
| Subject | Company A (9000) | Company B ( 7500) |
|---|---|---|
| R&D | 1300 | 1400 |
| Marketing | 1440 | 900 |
| Accounts | 860 | 500 |
| Production | 2000 | 1800 |
| HR | 1800 | 1500 |
| Finance | 1600 | 1400 |
- a) 700
b) 200
c) 400
d) 600
e) 900
- a) 600
b) 400
c) 500
d) 100
e) 800
- a) 1:9
b) 7:3
c) 4:9
d) 9:8
e) 3:2
- a) 10/4%
b) 50/3%
c) 26/7%
d) 12/6%
e) 43/6%
- a) 120%
b) 160%
c) 216%
d) 567%
e) 230%
| College | Total number of students | Percentage of arts students | Ratio of civil to mechanical engineering students |
|---|---|---|---|
| A | 1500 | 35% | - |
| B | - | 40% | - |
| C | - | - | 7:3 |
| D | 2100 | - | 3:2 |
| E | 1750 | - | - |
- a) 120
b) 430
c) 351
d) 320
e) 270
- a) 445:247
b) 441:243
c) 453:247
d) 441:247
e) 441:249
- a) 5 1/7%
b) 8 1/7%
c) 2 1/7%
d) 7 1/7%
e) 1 1/7%
- a) 1546
b) 1456
c) 1585
d) 1865
e) 1687
- a) 1050
b) 1205
c) 1640
d) 1550
e) 4520
| Days | Efficiency of Anand and Abinav | Time taken by both to complete work hours |
|---|---|---|
| Jan 1 | 3:2 | 3 |
| Jan 2 | 3:2 | 4 |
| Jan 3 | 7:9 | 6 |
| Jan 4 | 8:9 | 5 |
| Jan 5 | 5:4 | 8 |
- a) 115/2 hours
b) 111/13 hours
c) 108/19 hours
d) 110/19 hours
e) 110/13 hours
- a) 120/9 hours
b) 200/9 hours
c) 100/11hours
d) 210/11 hours
e) 150/21 hours
- a) 3/2 hours
b) 7/4 hours
c) 7/5 hours
d) 8/3 hours
e) 9/5 hours
- a) 3%
b) 5%
c) 8%
d) 15%
e) 6%
| A:F | 3:4 |
| B:G | 3:2 |
| C:H | 5:6 |
| D:I | 4:5 |
| E:J | 9:10 |
- a) 7 minutes
b) 169/36 minutes
c) 5 minutes
d) 178/39 minutes
e) None of these
- a) 4 minutes
b) 47/12 minutes
c) 39/10 minutes
d) 5 minutes
e) None of these
- a) 67.67%
b) 74.44%
c) 98.48%
d) 81.14%
e) 83.33%
- a) 4:5
b) 5:6
c) 6:7
d) 3:4
e) None of these
- a) 27/13 days
b) 41/27 days
c) 31/11 days
d) 51/29 days
e) None of these