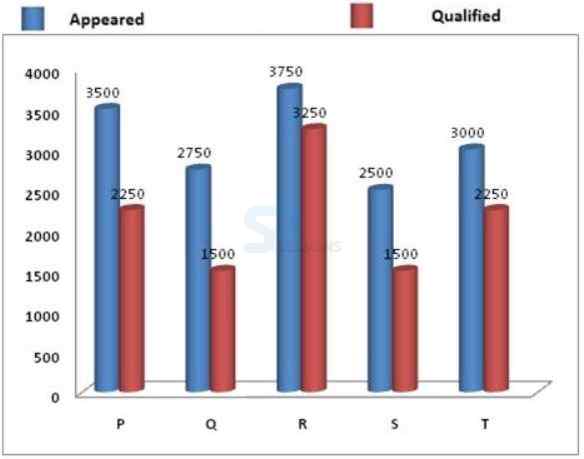
Directions[1-5]: Study the following graph carefully to answer the questions that follow:
Total number of students appeared and qualified from various colleges in a scholarship exam.

1. The average number of students qualified in the examination from colleges R and S is what per cent of the average number of students appeared for the examination from the same colleges?

A. 76% B. 65% C. 72% D. 56% E. None of these

2. What is the ratio of the total number of students appeared to the total number of students qualified in the scholarship exam from R and T?

A. 27 : 31 B. 21 : 23 C. 27 : 22 D. 17 : 23 E. None of these

3. What is the ratio of the number of students qualified in the scholarship examination from college P and the number of students qualified in the examination from college Q?

A. 5 : 7 B. 5 : 2 C. 1 : 2 D. 3 : 2 E. None of these

4. The number of students appeared for the scholarship exam from college S is approximately what percent of the total number of students appeared for the exam from all the colleges together?

A. 26.42% B. 12.62% C. 16.12% D. 18.25% E. None of these

5. What is the difference between the average number of students appeared in the scholarship exam from all the given colleges and the average number of students qualified from all the colleges together?

A. 950 B. 1250 C. 750 D. 1525 E. 1524

Answers and Explanations
1. Answer - Option A
Explanation -
Total number of students qualified in the examination from colleges R and S
= (3250 + 1500) = 4750
Average number of students qualified in the examination from colleges R and S
= [latex] \frac {4750}{2}[/latex] = 2375
Total number of students appeared in the examination from colleges R and S
= (3750 + 2500) = 6250
Average number of students appeared in the examination from colleges R and S
= [latex] \frac {6250}{2}[/latex] = 3125
Required percentage = [latex] \frac { (2375 \times 100)}{3125}[/latex] (2375*100) = 76%
2. Answer - Option C
Explanation -
Total number of students appeared in the scholarship exam from R and T
= (3750 + 3000) = 6750
Total number of students qualified in the scholarship exam from R and T
= (3250 + 2250) = 5500
Required ratio = [latex] \frac {6250}{5500}[/latex] = 27 : 22
3. Answer - Option D
Explanation -
Required ratio = [latex] \frac {2250}{1500}[/latex] = 3 : 2
4. Answer - Option C
Explanation -
Total number of students appeared for the scholarship exam from colleges = 2500
Total number of students appeared for the exam from all the colleges
= (3500 + 2750 + 3750 + 2500 + 3000) = 15500
Required percentage = [latex] \frac { (2500 \times 100)}{15500}[/latex] = 16.12%
5. Answer - Option A
Explanation -
Total number of students appeared for the exam from all the colleges
= (3500 + 2750 + 3750 + 2500 + 3000) = 15500
Average = [latex] \frac {15500}{5}[/latex] = 3100
Total number of students qualified for the exam from all the colleges
= (2250 + 1500 + 3250 + 1500 + 2250) = 10750
Average = [latex] \frac {10750}{5}[/latex] = 2150
Required difference = (3100 - 2150) = 950

Directions[1-3]: What should come in place of the question mark (?) in the following questions?
1. [latex]\sqrt {676} = \sqrt {225} + ?[/latex]

A. 11 B. 121 C. 22 D. 44 E. 55

2. [latex]\frac {3}{19} of \frac {6}{15} of 855 = ?[/latex]

A. 108 B. 54 C. 27 D. 81 E. 88

3. 672÷24×18+153-345= ?

A. 311 B. 322 C. 312 D. 308 E. 222

Direction[4-5]: In each question numbered I and II have been given. You have to solve both the equations and mark the appropriate option.
4. I. [latex]{X}^{2} - x - 6 = 0[/latex] II. [latex]{Y}^{2} - 6Y + 8 = 0[/latex]

A. X > Y B.X < Y C. X + Y D. X - Y E. X = Y or no relationship can be established

5. I. [latex]{X}^{2} + 11x + 30 = 0[/latex] II. [latex]{Y}^{2} + 7Y + 12 = 0[/latex]

A. X > Y B.X < Y C. X + Y D. X - Y E. X = Y or no relationship can be established

Answers and Explanations
1. Answer - Option A
Explanation -
[latex]\sqrt {676} = \sqrt {225} + ?[/latex]
26 = 15 + x
So x = 11
2. Answer - Option B
Explanation -
? = 855 × (6 ÷ 15) × (3 ÷ 19) = 54
Hence option B is correct
3. Answer - Option C
Explanation -
672 ÷ 24 × 18 + 153 - 345
504 + 153 -345 = 312
4. Answer - Option E
Explanation -
I. x=3,−2
II. Y=2, 4
Hence answer=(E)
5. Answer - Option B
Explanation -
From I,
[latex]{X}^{2} + 11x + 30 = 0[/latex]
[latex]{X}^{2} + 6X + 5X + 30 = 0[/latex]
X (X + 6) + 5(X + 6) = 0
(X + 6)(X + 5) = 0
X = -5, -6
From II,
[latex]{Y}^{2} + 7Y + 12 = 0[/latex]
[latex]{Y}^{2} + 4Y + 3(y - 4) = 0[/latex]
Y = -3, -4

1. Two brothers Adam, Shane started a company with an initial investment in the ratio 7:2. The company earned equal revenue for first the first and second year and the profit is divided equally between them every year. To equalise the initial investment Shane had to pay his entire share of revenue for the first year and half his share of revenue in the second year. Find the ratio of initial investment to total revenue.

A. 27 : 40 B. 20 : 3 C. 40 : 3 D. 3 : 40 E. None of these

2. If the numerator of a fraction is increased by 200% and the denominator is increased by 300%, the resultant fraction is 15/26. What was the original fraction?

A. [latex]\frac {8}{11}[/latex] B. [latex]\frac {10}{11}[/latex] C. [latex]\frac {9}{13}[/latex] D. [latex]\frac {10}{13}[/latex] E. [latex]\frac {12}{14}[/latex]

3. Four men can complete a piece of work in 40 days. Four women can complete the same work in 64 days. Find the time in which 10 men and 16 women working together can complete the same work?

A. 8 days B. 6 days C. 4 days D. 9 days E. None of these

4. The respective ratio between two numbers is 4: 7. If 4 is added to each of the two numbers, their respective ratio is 3 : 5. What is the larger number?

A. 42 B. 63 C. 56 D. 49 E. 50

5. 4% of 599.78 × 19.1919 ÷ (2.987 +1.004) =?

A. 111 B. 121 C. 114 D. 118 E. 124

Answers and Explanations
1. Answer - Option A
Explanation -
Let Adam’s investment be 7x
Shane’s investment = 2x
Let total revenue for two years be 2Y
Adam’s share in revenue = Y
Shane’s share in revenue = Y
Now to equalise initial investment [latex] \rightarrow 2x + \frac {Y}{2} + \frac {Y}{4} = 7x[/latex]
[latex]\frac {3Y}{4} = 5x \rightarrow \frac {x}{Y} = \frac {3}{20}[/latex]
Ratio of initial investment and total reveue= [latex]\frac {9x}{2Y} = \frac {27}{40}[/latex]
2. Answer - Option D
Explanation -
Let the original fraction be [latex] \frac {x}{y}[/latex]
Then according to questions
[latex] \frac {300x}{400y} = \frac {15x}{20y} = \frac {3x}{4y} [/latex]
[latex] \frac {3x}{4y} = \frac {15}{26} [/latex]
[latex] \frac {x}{y} = \frac {10x}{13y} [/latex]
3. Answer - Option A
Explanation -
4 men take 40 days to complete the work.
10 men would take = [latex]\frac {4 \times 40}{10}[/latex] = 16 days
Similarly, 16 women would take 16 days to complete it.
10 men as well as 16 women would take 16 days to complete it.
So, working together they would take [latex]\frac {16}{2}[/latex] = 8 days to complete it.
4. Answer - Option C
Explanation -
[latex]\frac {4x + 4}{7x + 4} = \frac {3}{5}[/latex]
x = 8
larger number = 7x = 56
hence option C is correct
5. Answer - Option C
Explanation -
4% of 600 = 24
2.987 + 1.004 = 4
[latex]\frac {24 × 19}{4}[/latex] = 456
6 × 19 = 114