Directions (1-5): Study the following information carefully and answer the questions given below:
In a college there are 1400 students who are doing graduation in any one of the subjects, out of the five different subjects viz. Zoology, Botany, Mathematics, Physics and Statistics. The ratio of the number of boys and girls among them is 6:8.30% of the total girls are doing graduation in Zoology and 20% of the total girls are doing graduation in Statistics. The total number of students doing graduation in Botany is 220. 250 students are doing graduation in Mathematics. The ratio of the number of girls and the number of boys doing graduation in Statistics is 2:1.20% of the total number of boys are doing graduation in Botany. The ratio of the number of girls and that of boys doing graduation in Mathematics is 2:3. There are an equal number of boys and girls doing graduation in Physics. 290 students are doing graduation in Zoology.
1. What is the total number of students doing graduation in physics and Statistics together?

A. 510 B. 540 C. 640 D. 620 E. 660

2. What is the ratio of the number of boys doing graduation in Mathematics and to a number of girls doing graduation in Botany?

A. 1:2 B. 3:1 C. 3:4 D. 3:2 E. 2:1

3. What is the difference between the number of boys doing graduations in Zoology and the number of girls doing graduation in Mathematics?

A. 50 B. 75 C. 60 D. 45 E. 55

4. In which of the following graduation courses, the number of the girls the highest and in which course is the number of boys is second lowest respectively?

A. Statistics and Zoology B. Zoology and Botany C. Physics and Statistics D. Zoology and Statistics E. Physics and Zoology

5. The number of girls doing graduation in Statistics is what percent of the number of boys doing graduation in physics?

A. 76% B. 75% C. 80% D. 81% E. 78%

Answers and Explanations
1. Answer - Option C
Explanation -
Number of boys = 600
Number of girls = 800

Required answer = 200 + 200 + 160 + 80 = 640
2. Answer - Option D
Explanation -
Required ratio = 150 : 100 = 3:2
3. Answer - Option A
Explanation -
Required difference = 100 - 50 = 50
4. Answer - Option D
Explanation -
Zoology and statistics
5. Answer - Option C
Explanation -
Required percentage = [latex]\frac {160}{200}[/latex] x 100 = 80%

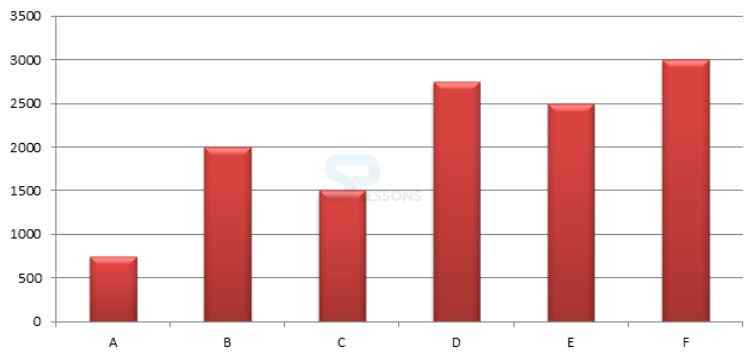
Directions (1 to 5): Following bar chart represents the number of people in 6 different villages (A, B, C, D, E and F) and the tabular column depicts the ratio of literate to illiterate people and percentage of male living in those villages.

Number of people living in six villages

1. If 40% of the female from village B is literate, then what is the percentage of male, who is illiterate from village B?

A. 38% B. 35% C. 37% D. Cannot be determined E. None of these

2. What is the percentage of literate people in all the six villages together?

A. 55% B. 53% C. 51% D. Cannot be determined E. None of these

3. What is the ratio between numbers of illiterate people from villages B, C & D to number of female from villages A, E & F?

A. 320:527 B. 527:330 C. 330:527 D. 527:320 E. None of these

4. If 3% of female from village D & 5% of female from village E are literate then what is the total number of literate male from D & F together?

A. 1823 B. 1723 C. 1623 D. Cannot be determined E. None of these

5. The number of female from villages A & C is how much percentage more or less than number of female from villages D & F?

A. 24.76% B. 24.72% C. 25.76% D. 25.72% E. None of these

Answers and Explanations
1. Answer - Option C
Explanation -
→ No. of illiterate female from village B = 60 % (700) = 420
→ No. of illiterate from village B = [latex](\frac {9}{20}) \times 2000 = 900[/latex]
Therefore,
→ No. of illiterate male from village B = 900 - 420 = 480
→ No. of male from village B = 65 %( 2000) = 1300
→ % of male, who is illiterate from village B = [latex](\frac {480}{1300}) \times 100 [/latex] = 36.9 ≈ 37
2. Answer - Option B
Explanation -
→ No. of Literate from village A = [latex](\frac {2}{5}) \times 750[/latex] = 300
→ No. of Literate from village B = [latex](\frac {11}{20}) \times[/latex] 2000 = 1100
→ No. of Literate from village C = [latex](\frac {13}{1}) \times[/latex] 1500 = 1300
→ No. of Literate from village D = [latex](\frac {4}{5}) \times[/latex] 2750 = 2200
→ No. of Literate from village E = [latex](\frac {1}{4}) \times[/latex] 2500 = 625
→ No. of Literate from village F = [latex](\frac {11}{30}) \times[/latex] 3000 = 1100
→ Total no. of literate in all villages= 300 + 1100 + 1300 + 2200 + 625 + 1100 = 6,625
→ Total no. of people in all villages= 750 + 2000 + 1500 + 2750 + 2500 + 1100 = 12,500
→ % of literate people in all villages = [latex](\frac {6625}{12500}) \times[/latex] 100 = 53 %
3. Answer - Option C
Explanation -
→ Illiterate from village B = 2000 - 1100 = 900
→ Illiterate from village C = 1500 - 1300 = 200
→ Illiterate from village D = 2750 - 2200 = 550
→ Female from village A = 48% (750) = 360
→ Female from village E = 61% (2500) = 1525
→ Female from village F = 25% (3000) = 750
→ Ratio = (900 + 200 + 550) : (360 + 1525 + 750) = 1650 : 2635 = 330 : 527 (ans)
4. Answer - Option D
Explanation -
→ Since we don’t have enough data for village F
→ We cannot determine the answer
5. Answer - Option A
Explanation -
→ Female from village A = 360
→ Female from village C = 825
→ Total = 1185
→ Female from village D = 825
→ Female from village F= 750
→ Total= 1575
→ Less% = [latex][\frac {(1575 – 1185)} {1575}] \times 100 = (\frac {390}{1575}) \times 100 = 24.76[/latex] %

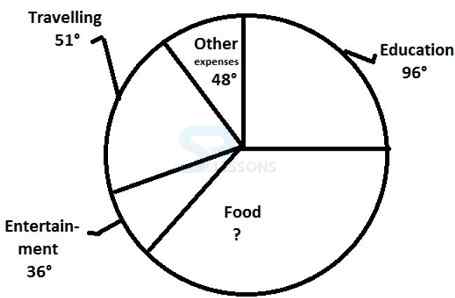
Directions (1 to 5): Study the following the pie-chart and table carefully to answer the questions given below:

The following pie-chart shows the distribution of the monthly family budget of a person.

The following table shows the further distribution (in percent) of the above-mentioned items among the five family members i.e P (the person himself), W (his wife), Rahul (son), Rohit (son), and Preeti (his daughter). His monthly family budget is Rs. 1,20,000

1. What is the average expenses of P?

A. Rs. 5620 B. Rs. 5644 C. Rs. 5640 D. Rs. 5460 E. Rs. 5480

2. What is the approximate percentage increase in the amount Which Rahul enjoys for entertainment as compared to Preeti for the same?

A. 33% B. 31% C. 34% D. 37% E. 35%

3. The average expenses of Rohit is approximately what percent of the average expenses of W (Wife)?

A. 76.4% B. 81.5% C. 79.5% D. 83.5% E. 89.5%

4. Find the difference (in percentage of the budget) between the average expenses of Education and the average expenses on Entertainment of the couple?

A. 1.3% B. 0.9% C. 2% D. 2.2% E. 2.5%

5. The total amount spent by Rahul on Travelling and Food is approximately what percent of the total amount spent by Preeti on Education and Food?

A. 150% B. 168% C. 171% D. 175% E. 174%

Answers and Explanations
1. Answer - Option
Explanation -
Average expenses of P
= (10% Of [latex]\frac {96}{360}[/latex] + 30 % of [latex]\frac {129}{360}[/latex] + 10% of [latex]\frac {36}{360}[/latex] + 40% of [latex]\frac {51}{360}[/latex] + 20% of [latex]\frac {48}{360}[/latex]) [latex]\times \frac {120000}{5}[/latex]
= [latex]\frac {960 + 3870 + 360 + 2040 + 960}{3600 } \times \frac {120000}{5}[/latex]
= Rs. 5460
2. Answer - Option A
Explanation -
Amount spent by Rahul on Entertainment
[latex]\frac {20}{100} \times \frac {36}{360} \times 120000 = Rs 2400[/latex]
Amount spent by Preeti on Entertainment
[latex]\frac {15}{100} \times \frac {36}{360} \times 120000 = Rs 1800[/latex]
∴ Required percentage increase
[latex]\frac {2400 - 1800}{1800} \times 100 = 33[/latex]%
3. Answer - Option D
Explanation -
Average expenses of Rohit
= [latex](25% Of [latex]\frac {96}{360}[/latex] + 15 % of [latex]\frac {129}{360}[/latex] + 25% of [latex]\frac {36}{360}[/latex] + 10% of [latex]\frac {51}{360}[/latex] + 10% of [latex]\frac {48}{360}[/latex]) [latex]\times[/latex] 120000
= [latex]\frac {2400 + 1935 + 900 + 510 + 480}{36000 } \times \frac {120000}{5}[/latex]
= Rs 4150
Average expenses of W (wife)
= [latex](15% 0f \frac {96}{360} + 25 % of \frac {129}{360} + 30% of \frac {36}{360} + 10% of \frac {51}{360} + 25% of \frac {48}{360}) \times \frac {120000}{5}[/latex]
= [latex]\frac {1440 + 3225 + 1080 + 510 + 1200}{36000} \times \frac {120000}{5}[/latex]
= Rs 4970
∴ Required percentage
= [latex]\frac {4150}{4970} \times 100 = 83.5[/latex]%
4. Answer - Option A
Explanation -
Required difference
= ((10 + 15) of [latex]\frac {96}{360}[/latex] - (30 + 10)% of [latex]\frac {36}{360}[/latex]) [latex]\times \frac {120000}{2}[/latex]
= [latex]\frac {2400 - 1440}{36000} \times \frac {120000}{5} = Rs.1600[/latex]
∴ Required percentage
= [latex]\frac {1600}{120000} \times 100 = 1.3[/latex]%
5. Answer - Option C
Explanation -
Required percentage
[latex]\frac {20 \times 129 + 25 \times 51}{960 + 1290} \times 100[/latex]
[latex]\frac {2580 + 1275}{960 + 1290} \times 100 = \frac {3855}{2250} \times 100 = 171[/latex]%