Directions (1-5): Study the following information carefully and answer the questions given below:

Classification of 100 Students Based on the Marks Obtained by them in Physics and Chemistry in an Examination.

1. What is the different between the number of students passed with 30 as cut-off marks in Chemistry and those passed with 30 as cut-off marks in aggregate?

A. 3 B. 4 C. 5 D. 6 E. 10

2. If at least 60% marks in Physics are required for pursuing higher studies in Physics, how many students will be eligible to pursue higher studies in Physics?

A. 27 B. 32 C. 34 D. 41 E. 45

3. The percentage of number of students getting at least 60% marks in Chemistry over those getting at least 40% marks in aggregate, is approximately?

A. 21% B. 27% C. 29% D. 31% E. 45%

4. The number of students scoring less than 40% marks in aggregate is?

A. 13 B. 19 C. 20 D. 27 E. 25

5. If it is known that at least 23 students were eligible for a Symposium on Chemistry, then the minimum qualifying marks in Chemistry for eligibility to Symposium would lie in the range?

A. 40-45 B. 30-40 C. 20-30 D. Below 20 E. Below 30

Answers and Explanations
1. Answer - Option D
Explanation -
Required difference
= (No. of students scoring 30 and above marks in Chemistry) - (Number of students scoring 30 and above marks in aggregate)
= 27 - 21
= 6.
2. Answer - Option B
Explanation -
We have 60% of 50 = [latex](\frac {60}{100} \times 50)[/latex] = 30
i.e, Required number
= No. of students scoring 30 and above marks in Physics
= 32
3. Answer - Option C
Explanation -
Number of students getting at least 60% marks in Chemistry
= Number of students getting 30 and above marks in Chemistry
= 21.
Number of students getting at least 40% marks in aggregate
= Number of students getting 20 and above marks in aggregate
= 73.
Required percentage = [latex](\frac {21}{73} \times 100)[/latex]%
= 28.77%
≈ 29%.
4. Answer - Option D
Explanation -
We have 40% of 50 = [latex](\frac {40}{100} \times 50)[/latex] = 20
i.e, Required number
= Number of students scoring less than 20 marks in aggreagate
= 100 - Number of students scoring 20 and above marks in aggregate
= 100 - 73
= 27.
5. Answer - Option C
Explanation -
Since 66 students get 20 and above marks in Chemistry and out of these 21 students get 30 and above marks, therefore to select top 35 students in Chemistry, the qualifying marks should lie in the range 20-30.

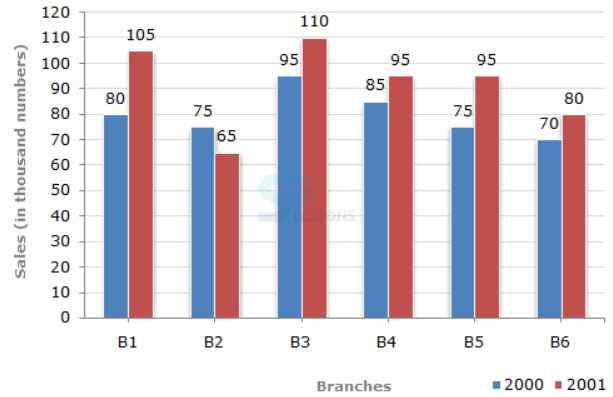
Directions (1 to 5): The bar graph given below shows the sales of books (in thousand number) from six branches of a publishing company during two consecutive years 2000 and 2001.

Sales of Books (in thousand numbers) from Six Branches - B1, B2, B3, B4, B5 and B6 of a publishing Company in 2000 and 2001.

1. What is the ratio of the total sales of branch B2 for both years to the total sales of branch B4 for both years?

A. 2:3 B. 3:5 C. 4:5 D. 7:9 E. 8:9

2. Total sales of branch B6 for both the years is what percent of the total sales of branches B3 for both the years?

A. 68.54% B. 71.11% C. 73.17% D. 75.55% E. 78.55%

3. What percent of the average sales of branches B1, B2 and B3 in 2001 is the average sales of branches B1, B3 and B6 in 2000?

A. 75% B. 77.5% C. 82.5% D. 87.5% E. 89.5%

4. What is the average sales of all the branches (in thousand numbers) for the year 2000?

A. 73 B. 80 C. 83 D. 88 E. 90

5. Total sales of branches B1, B3 and B5 together for both the years (in thousand numbers) is?

A. 250 B. 310 C. 435 D. 560 E. 570

Answers and Explanations
1. Answer - Option D
Explanation -
Required ratio = [latex]\frac {(75 + 65)}{(85 + 95)} = \frac {140}{180} = \frac {7}{9} [/latex]
2. Answer - Option C
Explanation -
Required percentage = [latex][\frac {(70 + 80)}{(95 + 110)} \times 100][/latex]%
= [latex][\frac {150}{205} \times 100][/latex]%
= 73.17%.
3. Answer - Option D
Explanation -
Average sales (in thousand number) of branches B1, B3 and B6 in 2000
= [latex]\frac {1}{3} \times (80 + 95 + 70) = (\frac {245}{3})[/latex].
Average sales (in thousand number) of branches B1, B2 and B3 in 2001
= [latex]\frac {1}{3} \times (105 + 65 + 110) = (\frac {280}{3})[/latex].
i.e, Required percentage = [latex][\frac {\frac {245}{3}}{\frac {280}{3}} \times] = (\frac {245}{280} \times 100)[/latex]% = 87.5%
4. Answer - Option B
Explanation -
Average sales of all the six branches (in thousand numbers) for the year 2000
= [latex]\frac {1}{6}[/latex] x [80 + 75 + 95 + 85 + 75 + 70]
= 80.
5. Answer - Option D
Explanation -
Total sales of branches B1, B3 and B5 for both the years (in thousand numbers)
= (80 + 105) + (95 + 110) + (75 + 95)
= 560.

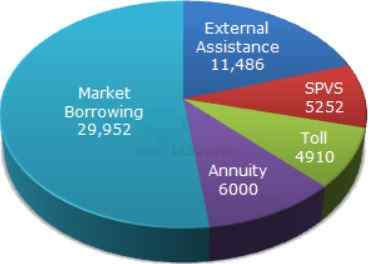
Directions (1 to 5): The following pie-chart shows the sources of funds to be collected by the National Highways Authority of India (NHAI) for its Phase II projects. Study the pie-chart and answers the question that follow.

Sources of funds to be arranged by NHAI for Phase II projects (in crores Rs.)

1. Near about 20% of the funds are to be arranged through:

A. SPVS B. External Assistance C. Annuity D. Market Borrowing E. None of these

2. If NHAI could receive a total of Rs. 9695 crores as External Assistance, by what percent (approximately) should it increase the Market Borrowing to arrange for the shortage of funds?

A. 4.5% B. 7.5% C. 6% D. 8% E. None of these

3. If the toll is to be collected through an outsourced agency by allowing a maximum 10% commission, how much amount should be permitted to be collected by the outsourced agency, so that the project is supported with Rs. 4910 crores?

A. Rs. 6213 crores B. Rs. 5827 crores C. Rs. 5401 crores D. Rs. 5316 crores E. None of these

4. The central angle corresponding to Market Borrowing is

A. 52° B. 137.8° C. 187.2° D. 192.4° E. None of these

5. The approximate ratio of the funds to be arranged through Toll and that through Market Borrowing is

A. 2 : 9 B. 1 : 6 C. 3 : 11 D. 2 : 5 E. None of these

Answers and Explanations
1. Answer - Option B
Explanation -
20% of the total funds to be arranged
= Rs. (20% of 57600) crores
= Rs. 11520 crores
≈ Rs. 11486 crores.
Rs. 11486 crores is the amount of funds to be arranged through External Assistance.
2. Answer - Option C
Explanation -
Shortage of funds arranged through External Assistance = Rs. (11486 - 9695) crores
= Rs. 1791 crores.
Therefore Increase required in Market Borrowing = Rs. 1791 crores.
Percentage increase required = [latex](\frac {1791}{29952} \times 100)[/latex]% = 5.98% ≈ 6%.
3. Answer - Option C
Explanation -
Amount permitted = (Funds required from Toll for projects of Phase II) + (10% of these funds)
= Rs. 4910 crores + Rs. (10% of 4910) crores
= Rs. (4910 + 491) crores
= Rs. 5401 crores.
4. Answer - Option C
Explanation -
Central angle corresponding to Market Borrowing = [latex](\frac {29952}{57600} \times 360°) = 187.2°[/latex]
5. Answer - Option B
Explanation -
Required ratio = [latex]\frac {4910}{29952} = \frac {1}{6.1} ≈ \frac {1}{6}[/latex]