1. The length of the longest rod that can be placed in a room which is 12 m long, 9 m broad and 8 m high is

A. 27 m B. 19 m C. 17 m D. 13 m

Answer - Option C
Explanation -
Length of the longest rod = Diagonal of the room
= [latex]\sqrt{{12}^{2} + {9}^{2} + {8}^{2}} [/latex]
[latex]\sqrt{289} [/latex] = 17
2. A circular well is dug to a depth of 14 metres with a diameter of 2 metres. What is the volume of the earth dug out ? ([latex]\pi = \frac{22}{7}[/latex])

A. 32 cubic metres B. 36 cubic metres C. 40 cubic metres D. 44 cubic metres

Answer - Option D
Explanation -
Required volume = Volume of right circle cylinder
= [latex] \pi {r}^{2}h[/latex]
[latex]\frac{22}{7} * 1 * 14 = 44 cubic meters[/latex]
3. The perimeter of one face of a cube is 20 cm. Its volume must be

A. 8000 [latex]{cm}^{3}[/latex] B. 1000 [latex]{cm}^{3}[/latex] C. 125 [latex]{cm}^{3}[/latex] D. 400 [latex]{cm}^{3}[/latex]

Answer - Option C
Explanation -
Volume of cube = [latex]{(Side of the cube)}^{3}[/latex]
[latex]{\frac{20}{4}}^{3}[/latex] = [latex]{5}^{3}[/latex] = 125 [latex]{(Side of the cube)}^{3}[/latex]
4. The curved surface of a right circular cone of height 15 cm and base diameter 16 cm is

A. 120 [latex]\pi {cm}^{2}[/latex] B. 60 [latex]\pi {cm}^{2}[/latex] C. 136 [latex]\pi {cm}^{2}[/latex] D. 68 [latex]\pi {cm}^{2}[/latex]

Answer - Option C
Explanation -
Here, h = 15 cm, r = 8 cm
i.e, Slant height, l = [latex]\sqrt{{h}^{2} + {r}^{2}} [/latex] = [latex]\sqrt{{15}^{2} + {8}^{2}} [/latex] = 17
Curved surface of the cone = πrl = π * 8 * 17 = 136 [latex]\pi {cm}^{2}[/latex]
5. The volume of a cube is V. The total length of its edges is

A. [latex]6{V}^{\frac{1}{3}}[/latex] B. 8 [latex]\sqrt{V} [/latex] C. [latex]12 {V}^{\frac{2}{3}}[/latex] D. [latex]12{V}^{\frac{1}{3}}[/latex]

Answer - Option D
Explanation -
There are 12 edges in the cube
Given : Volume = V
Each edge = [latex]{V}^{\frac{1}{3}}[/latex]
Total length of the edges = [latex]12{V}^{\frac{1}{3}}[/latex]
6. The cross-section of a canal is in the form of a trapezium. If canal top is 10 m wide, the bottom is 6 m wide and area of the cross section is 72 m2, then depth of the canal is

A. 10 m B. 7 m C. 6 m D. 9 m

Answer - Option D
Explanation -
Let h the height of the trapezium
Hence area of cross-section of the channel in the form of trapezium
[latex]\frac{1}{2}[/latex](10 + 6) * h = 72
i.e, 8h = 72
h = 9 m
7. A horse is tethered to one corner of a rectangular grassy field 40 m by 24 m with a rope 14 m long. Over how much area of the field can it graze ?

A. 154 [latex] {m}^{2}[/latex] B. 308 [latex] {m}^{2}[/latex] C. 150 [latex] {m}^{2}[/latex] D. None of these

Answer - Option A
Explanation -
Required area = shaded area
= [latex]\frac{1}{4} * \pi * {14}^{2}[/latex]
[latex]\frac{1}{4} * \frac{22}{7} * {14}^{2}[/latex] = 154 [latex] {m}^{2}[/latex]
8. The sides of a rectangular field are in the ratio 3 : 4 with its area as 7500 sq. m. The cost of fencing the field @ 25-paise per meter is

A. 87.50 B. 86.50 C. 67 .50 D. 55.50

Answer - Option A
9. A track is in the form of a ring whose inner circumference i s 352 m and the outer circumference is 396 m. The width of the track is

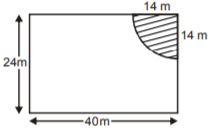
A. 44 m B. 14 m C. 22 m D. 7 m

Answer - Option D
Explanation -
Width of circular track = [latex]{r}_{1} - {r}_{2}[/latex]
= [latex]\frac{2 \pi {r}_{1} - 2 \pi {r}_{2} }{2 \pi} = \frac{396 - 352}{2 \pi}[/latex] = 7 m
10. A steel wire bent in the form of a square of area 121 [latex] {cm}^{2}[/latex]. If the same wire is bent in the form of a circle, then the area of the circle is

A. 130 [latex] {cm}^{2}[/latex] B. 136 [latex] {cm}^{2}[/latex] C. 154 [latex] {cm}^{2}[/latex] D. None of these

Answer - Option C
Explanation -
Side of a square = [latex]\sqrt{121} [/latex] = 11 cm
i.e, Perimeter of circle = 4 * 11 = 44 cm
2πr = 44
where r is radius of the circle
i.e, 2 * [latex]\frac{22}{7}[/latex] * r = 44
r = 7 cm
i.e, Area of the circle = π[latex] {r}^{2}[/latex] = [latex]\frac{22}{7} * {7}^{2} = 154{cm}^{2} [/latex]
11. The diameter of a garden roller is 1.4 m and it is 2 m long. How much area will it cover in 5 revolutions ?([latex]\pi = \frac{22}{7}[/latex])

A. 40 [latex]{m}^{3}[/latex] B. 44 [latex]{m}^{3}[/latex] C. 48 [latex]{m}^{3}[/latex] D. 36 [latex]{m}^{3}[/latex]

Answer - Option B
Explanation -
Garden roller is in the form of a cylinder whose radius is 0.7 m and height is 2 m.
i.e, Area covered in 5 revolutions
= 5 * 2πrh
= 5 * 2 * [latex]\frac{22}{7}[/latex] * 0.7 * 2
= 44 [latex]{m}^{3}[/latex]
12. The number of revolutions made by a wheel of diameter 56 cm in covering a distance of 1.1 km is ([latex]\pi = \frac{22}{7}[/latex])

A. 31.25 B. 56.25 C. 625 D. 62.5

Answer - Option C
Explanation -
Number of revolutions = [latex]\frac{1.1 * 1000 * 100}{2 * \frac{22}{7} * 28}[/latex] = 625
13. A bicycle wheel makes 5000 revolutions in moving 11 km. Find diameter of the wheel

A. 55 cm B. 60 cm C. 65 cm D. 70 cm

Answer - Option D
Explanation -
Circumference of the wheel = 2πr = [latex]\frac{11000 metres}{5000}[/latex]
πr = [latex]\frac{11}{10}[/latex]
r = [latex]\frac{11}{10} * \frac{7}{22} = \frac{7}{20}[/latex]metre
[latex]\frac{7}{20} * 100 [/latex] = 35 cm
Diameter of the wheel = 70 cm.
14. The perimeter of a rectangular field is 52 m. If the length of the field is 2m more than thrice the breadth, then what is the breadth of the field?

A. 6.5 m B. 6.215 m C. 13 m D. 6 m

Answer - Option D
Explanation -
Given, 2x + 2y = 52 ...(i)
and x = 3y + 2 .....(ii)
Solving (i) and (ii) we get
x = 20, y = 6
15. The sides of a triangle are in the ratio of [latex] \frac{1}{2} : \frac{1}{3}: \frac{1}{4}[/latex] If the perimeter is 52 cm, then the length of the smallest side is

A. 9 cm B. 10 cm C. 11 cm D. 12 cm

Answer - Option D
Explanation -
[latex] \frac{1}{2} : \frac{1}{3}: \frac{1}{4}[/latex] = 6a : 4a : 3a
13a = 52
a = 4,
smallest side = 3a = 12

1. The area of four walls of a room is 120 [latex]{m}^{2}[/latex]. The length is twice the breadth. If the height of the room is 4 m, find area of the floor.

A. 48 [latex]{m}^{2}[/latex] B. 49 [latex]{m}^{2}[/latex] C. 50 [latex]{m}^{2}[/latex] D. 52 [latex]{m}^{2}[/latex]

Answer - Option C
Explanation -
Using the formula, we get
2 × 4 (2b + b) = 120
b = 5
i.e, l = 10
Area = 50
2. A wire is looped in the form of a circle of radius 28cm. It is re-bent into a square form. Determine length of the side of the square.

A. 44 cm B. 45 cm C. 46 cm D. 48 cm

Answer - Option A
Explanation -
Given : R = 28
Circumference = 2[latex]\pi[/latex](28) = 176
Side of the square = [latex]\frac{176}{4}[/latex] = 44
3. A circular grassy plot of land, 42 m in diameter, has a path 3.5 m wide running round it on the outside. Find the cost gravelling the path at ₹ 4 per square metre.

A. ₹ 2002 B. ₹ 2003 C. ₹ 2004 D. ₹ 2000

Answer - Option D
Explanation -
Radius = 21
Required area = [latex]\pi[/latex]([latex]{(24.52)}^{2} - {(21)}^{2}[/latex]) = 500.5
Cost = 500.5 × 4 = 2002
4. A rectangular tank measuring 5 m × 4.5 m × 2.1 m is dug at the centre of the field measuring 13.5 m × 2.5 m. The earth dig out is spread evenly over the remaining portion of the field. How much is the level of the field raised?

A. 4.0 m B. 4.1 m C. 4.2 m D. 4.3 m

Answer - Option C
Explanation -
Area of field – Area of tank = 13.5 × 2.5 – 5 × 4.5
=11.25
Volume of tank = 41.25
i.e, Height raised = [latex]\frac{47 25}{11 25}[/latex] = 4.2
5. How many metres of cloth 5 m wide will be required to make a conical tent, the radius of whose base is 7 m and whose height is 25 m? (Take [latex]\pi[/latex] = 22/7)

A. 108 m B. 110 m C. 112 m D. 115 m

Answer - Option B
Explanation -
Given : l = 25
curved surface = [latex]\pi[/latex]rl
= [latex]\pi[/latex]× 7 × 25 = 550 [latex]{m}^{2}[/latex]
i.e, Length of the cloth = [latex]\frac{550}{5}[/latex] = 110
6. A metallic sheet is of rectangular shape with dimensions 48 × 36 cm. From each one of its corners, a square of 8 cm is cut off. An open box is made of the remaining sheet. Find volume of the box

A. 5110 [latex]{cm}^{3}[/latex] B. 5130 [latex]{cm}^{3}[/latex] C. 5120 [latex]{cm}^{3}[/latex] D. 5140 [latex]{cm}^{3}[/latex]

Answer - Option C
Explanation -
Dimensions of the box :
length = 48 – 16 = 32
width = 36 – 16 = 20
and height = 8
i.e, Volume = 32 × 20 × 8 = 5120
7. A room 5 m * 8 m is to be carpeted leaving a margin of 10 cm form each wall. If cost of the carpet is ₹ 18 per [latex]{m}^{2}[/latex], then cost of carpeting the room will be

A. ₹ 702.60 B. ₹ 691.80 C. ₹ 682.46 D. ₹ 673.92

Answer - Option D
Explanation -
Area of carpet = 7.8m × 4.8m = 37.44m2
Cost of Carpet = ₹ 18 × 37. 44 = ₹ 673.92
Hence option (d) is correct
8. A circle road runs around a circular garden. If difference between circumference of the outer circle and the inner circle is 44 m, then width of the road is

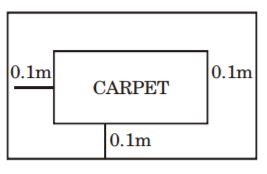
A. 4 m B. 7 m C. 3,5 m D. 7,5 m

Answer - Option B
Explanation -
2[latex]\pi({R}_{1} - {R}_{2})[/latex] = 44 [latex]\pi[/latex]
or [latex]({R}_{1} - {R}_{2})[/latex] = 7m
9. A garden is 24 m long and 14 m wide. There is a path 1 m wide outside the garden along its sides. If the path is to be constructed with square marble tiles 20 cm * 20 cm, the number of tiles required to cover the path is

A. 1800 B. 200 C. 2000 D. 2150

Answer - Option C
Explanation -
Area of path = (26 × 16) – (24 × 14) = 80 [latex]{m}^{2}[/latex]
Area of tile = 0.2 × 0.2 [latex]{m}^{2}[/latex]
i.e, Number of tiles = [latex]\frac{area of path}{area of one tile}[/latex]
= 2000 tiles
10. A lawn is in the form of an isosceles triangle. The cost of turfing it came to ₹ 1200 at ₹ 4 per [latex]{m}^{2}[/latex]. If the base is 40 m long, the length of each side is

A. 120 m B. 25 m C. 7.5 m D. None of these

Answer - Option B
Explanation -
area of triangle = [latex]\frac{1}{2}[/latex]bh
i.e, [latex]\frac{1}{2}[/latex] * 40 * h = 15 m
side = [latex]\sqrt{{20}^{2} + {15}^{2}} [/latex] = [latex]\sqrt{625} [/latex] = 25 m
11. The ratio of the rate of flow of water in pipes varies inversely as the square of the radius of the pipes. What is the ratio of the rates of flow in two pipes of diameters 2 cm and 4 cm ?

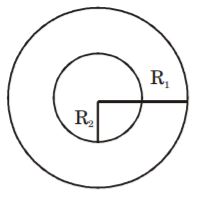
A. 1 : 2 B. 2 : 1 C. 1 : 8 D. 4 : 1

Answer - Option D
Explanation -
Ratio of two pipes are 1 cm and 2 cm squares of the Ratio of the two pipes are 1 cm and 4 cm.
i.e, Rates of flow of the two pipes are in the ratio
1 : [latex]\frac{1}{4}[/latex], i.e. 4 : 1.
12. A circle and a rectangle have the same perimeter. The sides of the rectangle are 18 cm and 26 cm. What is the area of the circle?

A. 88 [latex]{cm}^{2}[/latex] B. 154 [latex]{cm}^{2}[/latex] C. 1250 [latex]{cm}^{2}[/latex] D. 616 [latex]{cm}^{2}[/latex]

Answer - Option D
Explanation -
Perimeter of the rectangle = 2(18 + 26) = 88
= 2[latex]\pi[/latex]r
Hence r = 14.
Area of the circle = [latex]\pi[/latex]× [latex]{14}^{2}[/latex] = 616
13. A rectangular lawn 80 metres by 60 metres has two roads each 10 metres wide running in the middle of it, one parallel to the length and the other parallel to the breadth. Find the cost of gravelling them at ₹ 30 per square metre.

A. ₹ 39,000 B. ₹ 3,900 C. ₹ 3,600 D. ₹ 36,000

Answer - Option A
Explanation -
Cost = Area * rate
= [(80 * 10 + 60 * 10 ) – (10 * 10] * 30
= 39000.
14. The length of a room is double the breath. The cost of colouring the ceiling at ₹ 25 per sq m is ₹ 5,000 and the cost of painting the four walls at ₹ 240 per sq m is ₹ 64,800. Find the height of the room.

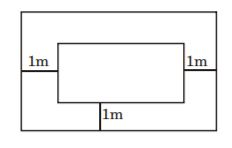
A. 4.5 m B. 4 m C. 3.5 m D. 5 m

Answer - Option A
Explanation -
Let the dimensions of the room be 2x and x.
Area of ceiling = 2x * x = [latex]\frac{5000}{25}[/latex] = 200
x = 10
i.e, Area of 4 walls = 2(lh + bh) = 2 (20h + 10h)
[latex]\frac{64800}{240}[/latex] = 270
Solving, we get h = 4.5 m
15. The trunk of a tree is a right cylinder 1.5 m in radius and 10 m high. The volume of the timber which remains when the trunk is trimmed just enough to reduce it to a rectangular parallelopiped on a square base is

A. 44 [latex]{m}^{3}[/latex] B. 46 [latex]{m}^{3}[/latex] C. 45 [latex]{m}^{3}[/latex] D. 47 [latex]{m}^{3}[/latex]

Answer - Option C
Explanation -
[latex]2{X}^{2}[/latex] = [latex]{3}^{2}[/latex]
[latex]{x}^{2}[/latex] = [latex]\frac{9}{2}[/latex]
i.e, V = Ibh = [latex]\frac{9}{2} * 10[/latex] = 45

1. A hemispherical bowl is filled to the brim with a beverage. The contents of the bowl are transferred into a cylindrical vessel whose radius is 50% more than its height. If the diameter is same for both the bowl and the cylinder, the volume of the beverage in the cylindrical vessel, as a per cent age of t he volume i n t he hemispherical bowl, is

A. [latex]66 \frac{2}{3}[/latex] % B. [latex]78 \frac{1}{2}[/latex] % C. 100 % D. more than 100%

Answer - Option C
Explanation -
Volume of hemisphere = [latex] \frac{2}{3} * \pi * {r}^{3}[/latex]
Volume of cylinder = [latex] \frac{2r}{3} * \pi * {r}^{2}[/latex]
Since the two are equal, the percentage is 100%.
2. In the accompanying figure, AB is one of the diameters of the circle and OC is perpendicular to it through the center O. If AC is 7 [latex]\sqrt{2} [/latex] cm, then what is the area of the circle in sq. cm.?

A. 24.5 B. 49 C. 98 D. 154

Answer - Option D
Explanation -
Let OA = OC = radius = r
[latex]O{A}^{2} + O{C}^{2} = A{C}^{2}[/latex]
[latex]{r}^{2} + {r}^{2} = {(7 \sqrt{2})}^{2} [/latex]
[latex]2{r}^{2} = 2 * 49[/latex]
r = 7
i.e, Area of the circle = [latex]\pi {r}^{2} = \frac {22}{7} * 49 = 154 {cm}^{2}[/latex]
3. A wire is in the form of a circle of radius 35 cm. If it is bent into the shape of a rhombus then what is the side of the rhombus?

A. 32 cm B. 70 cm C. 55 cm D. 17 cm

Answer - Option C
Explanation -
Circumference of the circle = 2[latex]\pi[/latex]r = [latex]2 * \frac{22}{7} * 35[/latex] = 200 cm
= Perimeter of the rhombus
i.e, Side of the rhombus = [latex]\frac{220}{4}[/latex] = 55 cm
4. A person wishes to make a 100 sqm rectangular garden. Since he has only 30 m barbed wire for fencing, he fences only three sides letting the house wall act as the fourth side. The width of the garden is

A. 10 m B. 5 m C. 50 m D. 100 m

Answer - Option B
Explanation -
Let width of the garden be x metres
i.e, Length of the garden = [latex]\frac{100}{x}[/latex]
i.e, [latex]\frac{100}{x}[/latex] + x + x = 30
[latex]{x}^{2}[/latex] – 15x + 50 = 0
x = 10, x = 5
x = 10 is omitted, because in that case, the garden will become square which is contrary to what is given
i.e, Width of the garden = 5 metres
5. The weight of a solid cone having diameter 14cm and vertical height 51 cm is ___, if the material of solid cone weighs 10 grams per cube cm.

A. 16.18 kg B. 17.25 kg C. 26.18 kg D. 71.40 kg

Answer - Option C
Explanation -
Volume of the solid cone = [latex]\frac{1}{3} * \pi * {7}^{2} * 51[/latex]
= [latex]\frac{1}{3} * \frac{22}{7} * 49 * 51[/latex] = 2618 [latex]{cm}^{3}[/latex]
i.e, Weight of the solid cone = (2618 * 10) gm.
= [latex]\frac{26180}{1000} kg[/latex] = 26.18 kg
6. In a special racing event , the per son who enclosed the maximum area would be the winner and would get ₹ 100 for every square metre of area covered by him/her. Johnson, who successfully completed the race and was the eventual winner, enclosed the area shown in figure below. What is the prize money won ? (Note: arc from C to D makes a complete semi-circle). AB = 3m, BC = 10m, CD = BE = 2m.

A. ₹ 2914 B. ₹ 2457 C. ₹ 2614 D. ₹ 2500

Answer - Option B
Explanation -
Area of the semi-circle = [latex]\frac{\pi}{2}[/latex] = 1.571 sq. m.
Area of the triangle = [latex]\frac{1}{2} * AB * BE[/latex]
= [latex]\frac{1}{2} * 3 * 2[/latex] = 3 sq. m.
Area of the rectangle = 10 * 2 = 20 sq. m.
i.e, Total area covered = 24.571 sq. m.
i.e, Prize money won by the person
= 24.571 * 100 = ₹ 2457
7. ABCD is a four-sided figure with AB parallel to CD and AD parallel to BC. ADE is right angle. If the perimeter of △ABE is 6 cm, then the area of the figure ABCD is

A. [latex]2 \sqrt{3} [/latex] sq. cm. B. [latex]4 \sqrt{3} [/latex] sq. cm. C. 3 sq. cm. D. None of these

Answer - Option C
8. It is required to fix a pipe such that water flowing through it at a speed of 7 metres per minute fills a tank of capacity 440 cubic metres in 10 minutes. The inner radius of the pipe should be

A. [latex]\sqrt{2}[/latex] m B. 2 m C. [latex]\frac {1}{2}[/latex] D. [latex]\frac {1}{\sqrt{2}}[/latex]

Answer - Option B
Explanation -
Explanation -
Volume of the pipe in one minute
= [latex] \pi * {r}^{2}(7) = \frac{440}{10} [/latex]
r = 2
9. Water flows out through a circular pipe whose internal diameter is 2 cm, at the rate of 6 metres per second into a cylindrical tank, the radius of whose base is 60 cm. By how much will be level of water rise in 30 minutes?

A. 2 m B. 4 m C. 3 m D. 5 m

Answer - Option C
Explanation -
Volume of water in the tank = [latex]\pi {(60)}^{2}[/latex] × x
where, x = level of the water
Water released by pipe in 30 minutes
= [latex]\pi * {1}^{2}[/latex] × 600 × 30 × 60
Equating the two and solving, we get
[latex]\pi {(60)}^{2}[/latex] × x = [latex]\pi * {1}^{2}[/latex] × 600 × 30 × 60
x = 300 cm = 3 m
10. A plot of land in the form of a rectangle has a dimension 240 m × 180 m. A drainlet 10 m wide is dug all around it (one the outside) and the earth dug out is evenly spread over the plot, increasing its surface level by 25 cm. The depth of the drainlet is

A. 1.225 m B. 1.229 m C. 1.227 m D. 1.223 m

Answer - Option C
Explanation -
Volume of the earth taken out = Volume of the earth on plot
= [{260 × 200} – {240 × 180}] × x
= 240 × 180 × [latex]\frac{1}{4}[/latex]
Solving, we get x = 1.227.
11. A square and an equilateral triangle have the same perimeter. If the diagonal of the square is [latex]12 \sqrt{2} [/latex] cm, then the area of the triangle is

A. [latex]24 \sqrt{3}{cm}^{2} [/latex] B. [latex]24 \sqrt{2}{cm}^{2} [/latex] C. [latex]64 \sqrt{3}{cm}^{2} [/latex] D. [latex]32 \sqrt{3}{cm}^{2} [/latex]

Answer - Option C
Explanation -
Let x be the side of the square.
i.e, [latex]{x}^{2} + {x}^{2} = {(12\sqrt {2})}^{2}[/latex]
x = 12
Now, perimeter of the equilateral triangle
= perimeter of the square
= 4x = 48 cm
i.e, Side of the equilateral triangle = [latex]\frac{48}{3}[/latex] = 16 cm
Area of equilateral triangle
= [latex]\frac{\sqrt{3}}{4} * {16}^{2} = 64 \sqrt{3}{cm}^{2} [/latex]
12. Semi-circular lawns are attached to both the edges of a rectangular field measuring 42 m * 35m. The area of the total field is

A. 3818.5 [latex]{m}^{2}[/latex] B. 8318 [latex]{m}^{2}[/latex] C. 5813 [latex]{m}^{2}[/latex] D. 1358 [latex]{m}^{2}[/latex]

Answer - Option A
Explanation -
Area B = Area D
Area C = Area E
Total area of the field
= Area of A + 2 * Area of B + 2 * Area of C
= 42 * 35 + 2 * [latex]\frac{}{} \pi {(21)}^{2} + 2 * \frac {1}{2}\pi {\frac({35}{2})}^{2}[/latex]
= 1470 + 1386 + 962.5
= 3818.5 [latex]{m}^{2}[/latex]
13. What is the area of the inner equilateral triangle if the side of the outermost square is ‘a’ ? (ABCD is a square)

A. [latex]\frac{3 \sqrt{3} {a}^{2}}{32}[/latex] B. [latex] \frac{3 \sqrt{3} {a}^{2}}{64}[/latex] C. [latex]\frac{5 \sqrt{3} {a}^{2}}{32}[/latex] D. [latex]\frac{\sqrt{3 {a}^{2}} }{64}[/latex]

Answer - Option A
14. An edge of a cube measures 10 cm. If the largest possible cone is cut out of this cube, then volume of the cone is

A. 260 [latex]{cm}^{3}[/latex] B. 260.9 [latex]{cm}^{3}[/latex] C. 261.9 [latex]{cm}^{3}[/latex] D. 262.7 [latex]{cm}^{3}[/latex]

Answer - Option C
Explanation -
Height of the cone = 10 cm
Radius of the base = [latex]\frac{10}{2}[/latex] cm = 5 cm
Hence volume of the largest possible cone cut out of this cube
= [latex]\frac{1}{3} * \frac{22}{7} * {(5)}^{2}* 10 = 261.8 {cm}^{3}[/latex]
15. In the figur e, ABCD is a square with side 10. BFD is an arc of a circle with centre C. BGD is an arc of a circle with centre A. What is the area of the shaded region ?

A. [latex]100 – 50 \pi[/latex] B. [latex]100 – 25 \pi[/latex] C. [latex]50 \pi - 100[/latex] D. [latex]25 \pi - 100[/latex]

Answer - Option C
Explanation -
Area of the portion DFBC = [latex]\frac{1}{4} * \pi * {(10)}^{2} = 25 \pi[/latex]
i.e, Area of △BCD = [latex]\frac{1}{2} * 10 * 10 = 50 [/latex]
i.e, Area of the portion DFBOD = Area of the portion DFBC – Area of △BCD
= 25[latex]\pi[/latex] – 50
i.e, Area of the portion DFBGD
= 2 * Area of the portion DFBOD
= 2(25[latex]\pi[/latex] – 50) = 50[latex]\pi[/latex] – 100