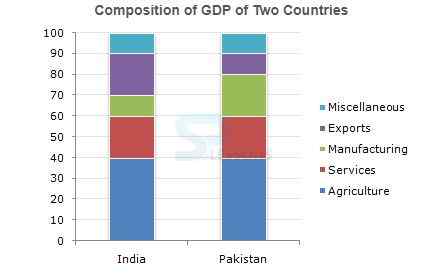
Directions: The following bar chart shows the composition of the GDP two countries (India and Pakistan).
1. If the total GDP of Pakistan is Rs. 10,000 crore, then a GDP accounted for by Manufacturing is ?

A. Rs.200 crore B. Rs.600 crore C. Rs.2,000 crore D. Rs.6,000 crore

Answer: Option C
Explanation: 20% of 10000 = 2000
2. What fraction of India's GDP is accounted for by Services?

A. ([latex]\frac{6}{33 }[/latex])th B. ([latex]\frac{1}{5 }[/latex])th C. ([latex]\frac{2}{3}[/latex])rd D. None of these

Answer: Option B
Explanation: Service accounts for 20%, i.e., ([latex]\frac{1}{5 }[/latex])th of the GDP of India.
3. If the total GDP of India is Rs.30,000 crores, then the GDP accounted for by Agriculture, Services and Miscellaneous is?

A. Rs.18,500 crore B. Rs.18,000 crore C. Rs.21,000 crore D. Rs.15,000 crore

Answer: Option C
Explanation: (40 + 20 + 10)% of 30,000 = Rs.21,000 crore.
4. Which country accounts for higher-earning out of Services and Miscellaneous together ?

A. India B. Pakistan C. Both spend equal amounts D. Cannot be determined

Answer: Option D
Explanation: Although the percentage of Services and Miscellaneous put together is equal for both the countries, we cannot comment on this since we have no data about the respective GDP's.
5. If the total GDP is the same for both the countries, then what percentage is Pakistan's income through agriculture over India's income through Services ?

A. 100 % B. 200 % C. 133.33 % D. None of these

Answer: Option A
Explanation: Since the GDP is same, the answer will be got by [latex]\frac{(40 - 20)}{20 }[/latex] = 100%.

1. A started a business with Rs.21,000 and is joined afterwards by B with Rs.36,000. After how many months did B join if the profits at the end of the year are divided equally?

A. 4 B. 5 C. 6 D. 7

Answer: Option B
Explanation: Suppose B joined after x months then, 21000*12=36000*(12-x) => 36x = 180 => x = 5
2. A, B and C invested Rs. 8000, Rs. 4000 and Rs. 8000 respectively in a business. A left after six months. If after eight months, there was a gain of Rs. 4005, then what will be the share of B?

A. Rs 690 B. Rs 790 C. Rs 890 D. Rs 990

Answer: Option C
Explanation: A:B:C = (8000*6):(4000*8):(8000*8) = 48:32:64 = 3:2:4 So B share = ([latex]\frac{2}{9}[/latex])*4005 = Rs 890
3. Nirmal and Kapil started a business investing Rs. 9000 and Rs. 12000 respectively. After 6 months, Kapil withdrew half of his investment. If after a year, the total profit was Rs. 4600, what was Kapil’s share initially ?

A. Rs 2300 B. Rs 2400 C. Rs 2500 D. None of above

Answer: Option A
Explanation: Nirmal:Kapil = 9000*12:(12000*6+6000*6) = 1:1 Kapils share = Rs. [4600 *([latex]\frac{1}{2}[/latex])) = Rs. 2300
4. Manoj received Rs. 6000 as his share out of the total profit of Rs. 9000 which he and Ramesh earned at the end of one year. If Manoj invested Rs.120000 for 6 months, whereas Ramesh invested his amount for the whole year, what was the amount invested by Ramesh

A. Rs. 2000 B. Rs. 3000 C. Rs. 4000 D. Rs. 5000

Answer: Option D
Explanation: Suppose Ramesh invested Rs. x. Then, Manoj : Ramesh = 20000 * 6 : x * 12. 120000/12x : [latex]\frac{6000}{3000}[/latex]6000/3000 => x = [latex]\frac{120000}{24}[/latex] = 5000
5. Yogesh started a business investing Rs. 45000. After 3 months, Pranab joined him with a capital of Rs. 60000. After another 6 months, Atul joined them with a capital of Rs. 90000. At the end of the year, they made a profit of Rs. 20000. What would be Atuls share in it?

A. Rs 7000 B. Rs 6000 C. Rs 5000 D. Rs 4000

Answer: Option D
Explanation: Just take care of the months of investment, rest all will be simple. Yogesh:Pranab:Atul = 45000*12:60000*9:90000*3 = 2:2:1 Atul's share = Rs. 20000 * ([latex]\frac{1}{5}[/latex]) = Rs. 4000

1. A sum of Rs. 1360 has been divided among A, B and C such that A gets [latex]\frac{2}{3}[/latex] of what B gets and B gets [latex]\frac{1}{4}[/latex] of what C gets. B's share is:

A. Rs. 120 B. Rs. 160 C. Rs. 240 D. Rs. 300

Answer: Option C
Explanation: Let C's share = Rs. x Then, B's share = Rs. [latex]\frac{X}{4 }[/latex] A's share = Rs. [latex]\frac{2}{3 }[/latex] X [latex]\frac{X}{4 }[/latex] = Rs. [latex]\frac{X}{6 }[/latex] [latex]\frac{X}{6 }[/latex] + [latex]\frac{X}{4 }[/latex] + x = 1360 [latex]\frac{17X}{12 }[/latex] = 1360 x = [latex]\frac{1360 × 12}{17 }[/latex] = Rs. 960 Hence, B's share = Rs. [latex]\frac{960}{4 }[/latex] = Rs. 240
2. A boat can travel with a speed of 13 km/hr in still water. If the speed of the stream is 4 km/hr, find the time taken by the boat to go 68 km downstream.

A. 2 hours B. 3 hours C. 4 hours D. 5 hours

Answer: Option C
Explanation: Speed downstream = (13 + 4) km/hr = 17 km/hr. Time is taken to travel 68 km downstream = [latex]\frac{68}{17 }[/latex] hrs = 4 hrs
3. A man's speed with the current is 15 km/hr and the speed of the current is 2.5 km/hr. The man's speed against the current is:

A. 8.5 km/hr B. 9 km/hr C. 10 km/hr D. 12.5 km/hr

Answer: Option C
Explanation: Man's rate in still water = (15 - 2.5) km/hr = 12.5 km/hr. Man's rate against the current = (12.5 - 2.5) km/hr = 10 km/hr.
4. In one hour, a boat goes 11 km/hr along the stream and 5 km/hr against the stream. The speed of the boat in still water (in km/hr) is:

A. 3 km/hr B. 5 km/hr C. 8 km/hr D. 9 km/hr

Answer: Option C
Explanation: Speed in still water = [latex]\frac{1}{2 }[/latex] (11 + 5) kmph = 8 kmph
5. A man can row at 5 kmph in still water. If the velocity of current is 1 kmph and it takes him 1 hour to row to a place and comes back, how far is the place?

2.4 km B. 2.5 km C. 3 km D. 3.6 km

Answer: Option C
Explanation: Speed downstream = (5 + 1) kmph = 6 kmph. Speed upstream = (5 - 1) kmph = 4 kmph. Let the required distance be x km. Then, [latex]\frac{X}{6 }[/latex] + [latex]\frac{X}{4 }[/latex] = 1 ⇒ 2x + 3x = 12 ⇒ 5x = 12 ⇒ x = 2.4 km.