Introduction
Introduction
In mathematics, there’s a concept for dealing with situations where size matters more than sign. It’s called absolute value. The absolute value of a number is its value regardless of its sign.
Quantitative Aptitude -BANKING|SSC|RAILWAYS|INSURANCE|RECRUITMENT EXAMS - EBOOKS
 Methods
Methods
Absolute value of a number is described as the distance from the origin to the number on a number line. The absolute value of a number N, denoted by N , is defined to be N if N is positive or zero and –N if N is negative.
Absolute value can be explored both numerically and graphically.
Absolute Value - the Numeric Approach -
Numerically, absolute value is indicated by enclosing a number, variable, or expression inside two vertical bars, like so:
|30|
|x|
|5n - 8|
Examples:
1. [latex]\mid{\frac{1}{2}}\mid[/latex] = [latex]\frac{1}{2}[/latex]
2. [latex]\mid{0}\mid[/latex] = 0
3. [latex]\mid{-2.6}\mid[/latex] = -(-2.6) = 2.6
Note that the absolute value of a number cannot be negative.
The description of absolute value as a distance and the formal definition are both explaining exactly what the most majority consider for absolute value. Utilizing distance as an approach to explain absolute value just implies that the answer will never be negative since distance is never going to be negative.
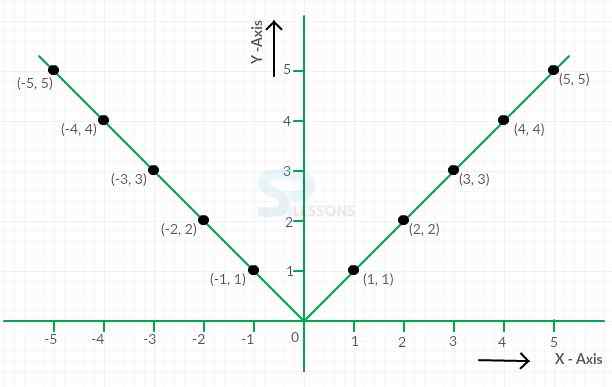
Absolute Value—the Graphic Approach
If [latex]a[/latex] is a real number([latex]n[/latex]), the absolute value of [latex]a[/latex] is denoted as [latex]\mid{a}\mid[/latex] then
[latex]\mid{a}\mid[/latex] = [latex]a[/latex] if [latex]a[/latex] ≥ 0 and [latex]a[/latex] if -[latex]a[/latex] < 0
Consider the following two dimensional graph and ([latex]x[/latex], [latex]y[/latex]) pair of values as coordinates.
If [latex]X[/latex] is a real number then
[latex]\mid{X}\mid[/latex] = [latex]X[/latex] if [latex]X[/latex] > 0;
[latex]\mid{X}\mid[/latex] = -[latex]X[/latex] if [latex]X[/latex] < 0;
[latex]\mid{X}\mid[/latex] = 0 if [latex]X[/latex] = 0.
Absolute values as a function i.e. [latex]y[/latex] = [latex]\mid{x}\mid[/latex].
From the graph their absolute values are tabulated as below:
So, minimum value of [latex]y[/latex] is zero.
Example: For instance both the points with the coordinate -7 and the point +7 are 7 units from the origin.
So, [latex]\mid{-7}\mid[/latex] = 7
[latex]\mid{7}\mid[/latex] = 7
Distance between - 7 to 7 is [latex]\mid{-7}\mid[/latex] + [latex]\mid{7}\mid[/latex] = 14
| [latex]y[/latex] | [latex]x[/latex] |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 0 | 0 |
| 3 | -3 |
| 2 | -2 |
| 1 | -1 |
Note:-
[latex]\mid{x}\mid[/latex] ≥ 0 is always true. On number line, [latex]\mid{x}\mid[/latex] is the number of units of distance between the point with co-ordinate [latex]x[/latex] and origin, regardless of whether the point is to be right or left to origin.
 Formulae
Formulae
If [latex]x[/latex], [latex]y[/latex] are real numbers. Then,
1. [latex]\mid{x . y}\mid[/latex] = [latex]\mid{x}\mid[/latex] [latex]\mid{y}\mid[/latex]
2. [latex]\mid{\frac{x}{y}}\mid[/latex] = [latex]\frac{\mid{x}\mid}{\mid{y}\mid}[/latex]
3. [latex]\mid{x + y}\mid[/latex] = [latex]\mid{x}\mid[/latex] + [latex]\mid{y}\mid[/latex]
If either both [latex]x[/latex], [latex]y[/latex] are positive values or both [latex]x[/latex], [latex]y[/latex] are negative values (or one of them is 0).
4. If one value is positive and another is negative. Then
[latex]\mid{x + y}\mid[/latex] < [latex]\mid{x}\mid[/latex] + [latex]\mid{y}\mid[/latex]
5. [latex]\mid{x - y}\mid[/latex] = [latex]\mid{x}\mid[/latex] - [latex]\mid{y}\mid[/latex]
If either both [latex]x[/latex], [latex]y[/latex] are positive values or both [latex]x[/latex], [latex]y[/latex] are negative values (or one of them is 0).
6. If one value is positive and another is negative. Then
[latex]\mid{x - y}\mid[/latex] > [latex]\mid{x}\mid[/latex] - [latex]\mid{y}\mid[/latex]
i.e. General rule for this is [latex]\mid{x + y}\mid[/latex] ≤ [latex]\mid{x}\mid[/latex] + [latex]\mid{y}\mid[/latex]
Similarly [latex]\mid{x - y}\mid[/latex] ≥ [latex]\mid{x}\mid[/latex] - [latex]\mid{y}\mid[/latex]
This can also be generalized as:
[latex]\mid{a_{1} + a_{2} + a_{3} + ....... + a_{n}}\mid[/latex] ≤ [latex]\mid{a_{1}}\mid + \mid{a_{2}}\mid + \mid{a_{3}}\mid + ........ + \mid{a_{n}}\mid[/latex]
Also, [latex]\mid{a_{1} - a_{2} - a_{3} - ....... - a_{n}}\mid[/latex] ≥ [latex]\mid{a_{1}}\mid - \mid{a_{2}}\mid - \mid{a_{3}}\mid - ........ - \mid{a_{n}}\mid[/latex]
Rules:
1. [latex]\mid{x}\mid[/latex] = α where α > 0 then direct solution will be
[latex]x[/latex] = + α or [latex]x[/latex] = - α
2. If [latex]\mid{x}\mid[/latex] < α where α > 0 then direct solution will be
- α < [latex]x[/latex] < α or [latex]x[/latex] ε (α, -α)
3. If [latex]\mid{x}\mid[/latex] ≤ α then direct solution will be
- α ≤ [latex]x[/latex] ≤ α or [latex]x[/latex] ε [α, -α]
4. If [latex]\mid{x}\mid[/latex] > α then direct solution will be
I. [latex]x[/latex] > α or [latex]x[/latex] < -α
II. [latex]x[/latex] ε (-∞, -α) U (α, ∞)
5. If [latex]\mid{x}\mid[/latex] ≥ α then direct solution will be
[latex]x[/latex] ≥ α or [latex]x[/latex] ≤ -α or [latex]x[/latex] ε (-∞, -α] U[α, ∞)
6. If [latex]\mid{x}\mid[/latex] =[latex]\mid{y}\mid[/latex]
Where [latex]\mid{x}\mid[/latex], [latex]\mid{y}\mid[/latex] are variables.
Then direct solution will be [latex]\mid{x}\mid[/latex] = [latex]\mid{y}\mid[/latex] or [latex]\mid{x}\mid[/latex] = -[latex]\mid{y}\mid[/latex] are two distinct solutions.
 Samples
Samples
1. Solve the inequality [latex]\mid{3x + 5}\mid[/latex] < 3
Solution:
A. The quantity on the left is greater.
B. The quantity on the right is greater.
C. Both are equal.
D. The relationship cannot be determined without further information.
Solution:
A. The quantity on the left is greater.
B. The quantity on the right is greater.
C. Both are equal.
D. The relationship cannot be determined without further information.
Solution:
- Given expression is [latex]\mid{3x + 5}\mid[/latex] < 3
⇒ -3 < 3[latex]x[/latex] + 5 < 3
⇒ - 3 - 5 < 3[latex]x[/latex] + 5 - 5 < 3 - 5
⇒ -8 < 3[latex]x[/latex] < -2
Divide by 3
⇒ [latex]\frac{-8}{3}[/latex] < [latex]\frac{3x}{3}[/latex] < [latex]\frac{-2}{3}[/latex]
⇒ [latex]\frac{-8}{3}[/latex] < [latex]x[/latex] < [latex]\frac{-2}{3}[/latex]
Therefore, [latex]x[/latex] ε ([latex]\frac{-8}{3}[/latex], [latex]\frac{-2}{3}[/latex])
- Given that
[latex]\mid{2x + 7}\mid[/latex] ≥ 21
2[latex]x[/latex] + 7 ≥ 21
2[latex]x[/latex] ≥ 21 - 7
2[latex]x[/latex] ≥ 14
[latex]x[/latex] ≥ 7 ............(I)
Or
2[latex]x[/latex] + 7 ≤ - 21
2[latex]x[/latex] ≤ - 21 - 7
[latex]x[/latex] ≤ -14 ............(II)
From equations(I) and (II)
[latex]x[/latex] ε (-∞, -14] U[7, ∞)
- Given that
[latex]\mid{3x + 7}\mid[/latex] = [latex]\mid{2x - 11}\mid[/latex]
3[latex]x[/latex] + 7 = 2[latex]x[/latex] - 11
3[latex]x[/latex] - 2[latex]x[/latex] = - 7 - 11
[latex]x[/latex] = -18 ........(I)
Or
3[latex]x[/latex] + 7 = -(2[latex]x[/latex] - 11)
3[latex]x[/latex] + 7 = -2[latex]x[/latex] + 11
3[latex]x[/latex] + 2[latex]x[/latex] = + 11 - 7
5[latex]x[/latex] = 4
[latex]x[/latex] = [latex]\frac{4}{5}[/latex] ........(II)
Therefore, [latex]x[/latex] = -18 and [latex]\frac{4}{5}[/latex]
| Quantity A | Quantity B |
| [latex]x[/latex] | 4 |
- Consider [latex]\mid{2x - 3}\mid[/latex] ≤ 1
-1 ≤ 2[latex]x[/latex] - 3 ≤ 1
Add 3
- 1 + 3 ≤ 2[latex]x[/latex] - 3 + 3 ≤ 1 + 3
2 ≤ 2[latex]x[/latex] ≤ 4
Divide by 2
[latex]\frac{2}{2}[/latex] ≤ [latex]\frac{2x}{2}[/latex] ≤ [latex]\frac{4}{2}[/latex]
1 ≤ [latex]x[/latex] ≤ 2
[latex]x[/latex] ε [1, 2]
Hence option B is correct.
| Column A | Column B |
| Maximum value of f([latex]x[/latex]) | 25 |
- Consider f([latex]x[/latex]) = 25 - [latex]\mid{x + 8}\mid[/latex]
It can have maximum value if [latex]x[/latex] = -8
Maximum value of f([latex]x[/latex]) = 25 - [latex]\mid{- 8 + 8}\mid[/latex] = 25
Therefore, correct option is C.