Bar graph: Presenting the given data in the form of horizontal and vertical bars by selecting a particular scale is called bar graph.

• One of the parameters is plotted on horizontal axis and the other on the vertical axis.


• The length of the bar shows the magnitude of the data, while its width is insignificant.

Types of bar graphs: Bar graphs are of five types. They are
1. Simple bar graphs:

• Bars are arranged in time sequence or the size of the variable.


• The length of each bar depends upon the size of the items.


• In simple bar graphs only one category of data is shown.

2. Sub - divided bar diagram:

• Different components of a total is represented.


• Bars are sub divided into a number component parts.

First, a bar representing the total is drawn, then it is divided into various segments, each representing a component of the total. Different shades or colours are used to represent different components.
3. Percentage bar diagram:

• Components are represented on percentage basis and it is like sub divided bar graph.


• All bars will be of same height.


• Used to highlight the relative importance of various components of the whole. Helpful to conclude the relative changes of the data.

4. Multiple bar graphs:

• Two or more bars are represented, adjoining each other, to represent different components of a related variable.


• Length of each bar represents the magnitude of the data.


• Total bars of one set are continuous, are separated from other set by a gap.


• When the number of related variables is more than one or where changes in the actual values of the component figures are significant.

5. Deviation Bar graphs:

• This represents net quantities. For example net profit or loss, net of imports and exports, which have both negative and positive values.


• Bars are represented like positive deviations are above the base-line while negative deviations are below the base-line.

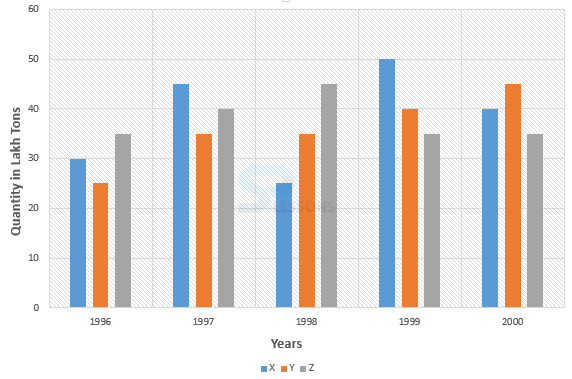
1. The data of the production of paper (in lakh tonnes) by three different companies X, Y and Z over the years are provided in the below bar graph. Read the graph carefully and answer the questions mentioned?

1. Which of the following years, the percentage rise/fall in production from the previous year is the maximum for company Y ?

(A) 1997 (B) 1998 (C) 1999 (D) 2000 (E) 1997 and 2000

2. What is the ratio of the average production of company X in the period 1998 - 2000 to the average production of company Y in the same period?

(A) 1 : 1 (B) 15 : 17 (C) 23 : 25 (D) 27 : 29 (E) None of these

3. What is the percentage increase in the production of company Y from 1996 to 1999?

(A) 30% (B) 45% (C) 50% (D) 60% (E) 75%

4. What is the difference between the production of company Z in 1998 and company Y in 1996?

(A) 2,00,000 tons (B) 20,00,000 tons (C) 20,000 tons (D) 2,00,00,000 tons (E) None of these

Solution:

1. Percentage change (rise/fall) in the production of company Y in the comparison to the previous year, for different years are:
In 1997 = [latex]\frac{(32 - 25)}{25} * 100[/latex]% = 40%
In 1998 = [latex]\frac{(35 - 35)}{25} * 100[/latex]% = 0%
In 1999 = [latex]\frac{(40 - 35)}{35} * 100[/latex]% = 14.29%
In 1997 = [latex]\frac{(50 - 40)}{40} * 100[/latex]% = 25%
Therefore, the maximum percentage rise/fall in the production of company Y is in 1997
So, option (A) is correct.
2. Average production of company X in the period 1998 - 2000 = [latex]\frac{1}{3} * (25 + 40 + 50)[/latex] =[latex]\frac{115}{3}[/latex] lakh tons.
Average production of company Y in the period 1998 - 2000 = [latex]\frac{1}{3} * (35 + 40 + 50)[/latex] =[latex]\frac{125}{3}[/latex] lakh tons.
Therefore, required ratio = [latex]\frac{\frac{115}{3}}{\frac{125}{3}}[/latex] = [latex]\frac{115}{125}[/latex]
So, option (C) is correct answer.
3. Percentage increase in the production of company Y from 1996 to 1999 = [latex]\frac{40 - 25}{25} * 100[/latex]% = [latex]\frac{15}{25} * 100[/latex]% = 60%
So, option (D) is correct answer.
4. Required difference = (45 - 25) x 100000 = 20,00,000 tons.
So, option (B) is the correct answer.

2. Number of people (in thousand) using three different types of mobile services over the years are given in the graph. Study the given graph and answer the given questions.

1. What is the average number of people using mobile service M for all the years together?

(A) 16 [latex]\frac{2}{3}[/latex] (B) 14444 [latex]\frac{1}{6}[/latex] (C) 16666[latex]\frac{2}{3}[/latex] (D) All of these. (E) None of these.

2. The total number of people using all the three mobile services in the year 2007 is what percent of the total number of people using all the three mobile services in the year 2008?

(A) 89.72 (B) 93.46 (C) 88.18 (D) 91.67 (E) None of these.

3. What is the respective ratio of number of people using mobile service L in the year 2005 to those using the same service in the year 2004?

(A) 8 : 7 (B) 3 : 2 (C) 19 : 13 (D) 15 : 11 (E) none of these.

Solution:

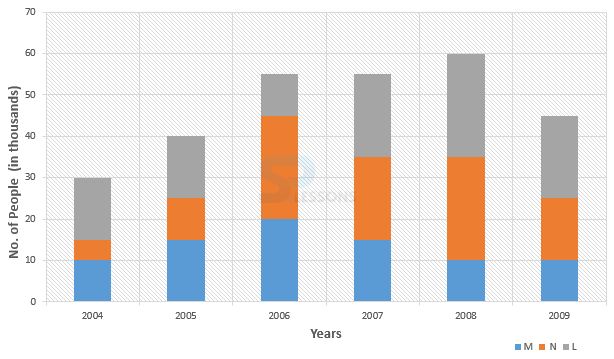
1. Average number of people using mobile service = [latex]\frac{5 + 10 + 25 + 20 + 25 + 15}{6}[/latex] thousand
= [latex]\frac{100}{6}[/latex] thousand = 16666[latex]\frac{2}{3}[/latex]
2. The percent = 16666[latex]\frac{2}{3}[/latex] = 91.67
3.The ratio = 15 : 10 = 3 : 2

3. Study the following graph carefully and answer the given questions given below:

1. What is the ratio of total imports to the total exports for all the given years together?

(A) 31 : 35 (B) 35 : 31 (C) 65 : 63 (D) 63 : 65 (E) None of these.

2. During which year the percentage rise/fall in imports from the previous year is the lowest?

(A) 1994 (B) 1998 (C) 1997 (D) 1995 (E) None of these.

Solution:

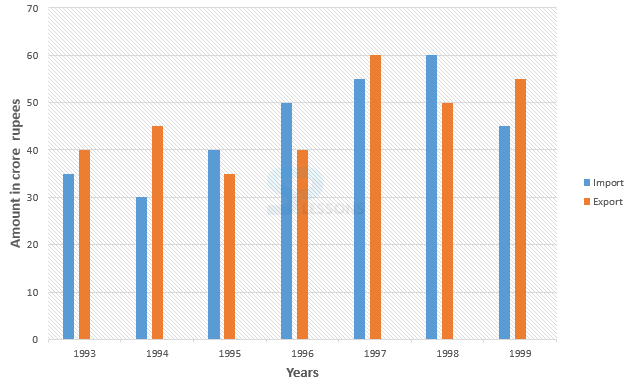
1. Total imports = 35 + 30 + 40 + 50 + 55 + 60 + 45 = 315 croes.
Total exports = 40 + 45 + 35 + 40 + 60 + 50 + 55 = 325crores.
Therefore, required ratio = 315 : 325 = 63 : 65
Hence, correct option is (D)
2. From the graph, the percentage rise in 1998 is the lowest.
Hence, correct option is (B)

4. The bar graph given below shows the foreign exchange reserves of a country (in million US $) from 1991-92 to 1998-99. Answer the below given questions?

1. What was the percentage increase in the foreign exchange reserves in 1997-1998 over 1993-94?

(A) 100 (B) 150 (C) 200 (D) 620 (E) 2520

2. The ratio of the number of years, in which the foreign exchange reserves are above the average reserves, to those in which the reserves are below the average reserves is?

(A) 2 : 6 (B) 3 : 4 (C) 3 : 5 (D) 4 : 4 (E) 5 : 3

Solution:

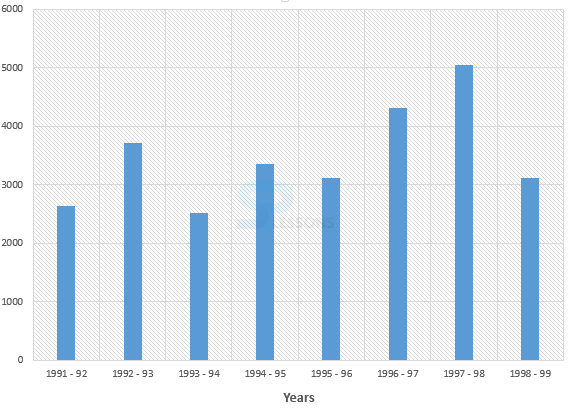
1. Foreign exchange reserves in 1997-98 = 5040 million US $
Foreign exchange reserves in 1993-94 = 2520 million US $
So, increase = 5040 - 2520 = 2520 million US $.
Therefore, percentage increase = [latex]\frac{2520}{2520} * 100[/latex]% = 100%
2. Average foreign exchange reserves over the given period = 3480 million US $.
The country had reserves above 3480 million US $ during the years 1992-93, 1996-97 and 1997-98 i.e. 3 years and below 3480 million US $ during the yeas 1991-92, 1993-94, 1994-95, 1995-96 and 1998-99 i.e. for 5 years. Therefore, required ratio = 3 : 5.

5. Out of two graphs provided below, one shows amount invested by a company in purchasing raw materials over the years and the other shows values of finished goods sold by the company over the years.
Study the two graphs and answer the below questions.


1. What was the difference between the average amount invested in raw materials during the given period and the average value of sales of finished goods during this period?

(A) Rs. 62.5 lakhs (B) Rs. 68.5 lakhs (C) Rs. 71.5 lakhs (D) Rs. 77.5 lakhs (E) Rs. 83.5 lakhs

2. In which year, there has been maximum percentage increase in the amount invested in raw materials as compared to the previous year?

(A) 1996 (B) 1997 (C) 1998 (D) 1999 (E) 2000

3. The value of sales of finished goods in 1999 was approximately what percent average amount invested in raw materials in the years 1997, 1998 and 1999?

(A) 33% (B) 37% (C) 45% (D) 49% (E) 53%

Solution:

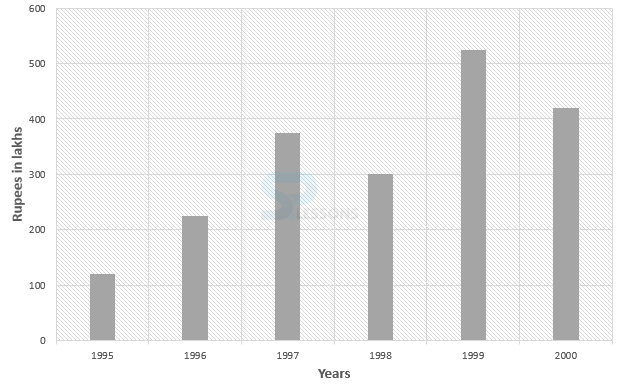
1. Required difference = Rs. [latex]\frac{1}{6} * (2 + 300 + 500 + 400 + 600 + 460)[/latex] - [latex]\frac{1}{6}(120 + 225 + 375 + 330 + 525 + 420)[/latex] lakhs
= Rs. [latex]\frac{2460}{6}[/latex] - [latex]\frac{1995}{6}[/latex] lakhs
= Rs. (410 - 332.5) lakhs
= Rs. 77.5 lakhs.
So, correct option is (D).
2. The percentage increase in the amount invested in raw-materials as compared to the previous year, for different years are:
In 1996 = [latex]\frac{225 - 120}{120} * 100[/latex]% = 87.5%
In 1997 = [latex]\frac{375 - 225}{225} * 100[/latex]% = 66.67%
In 1998 there is decrease.
In 1999 = [latex]\frac{525 - 330}{330} * 100[/latex]% = 59.09%
In 2000 there is decrease.
Therefore, maximum % increase is in 1996.
So, the correct option is (A).
3. Required percentage = [latex]\frac{600}{375 + 330 + 525} * 100[/latex]% = 48.78% = 49%
So, the correct option is (D).