Introduction
Introduction
A circle is a set of points that equidistant from a fixed point and the point from which all the points on a circle are equidistant is called the center of the circle and represented by letter 'O'. The distance from that point to the circle is called the radius of the circle.
Quantitative Aptitude -BANKING|SSC|RAILWAYS|INSURANCE|RECRUITMENT EXAMS - EBOOKS
 Methods
Methods
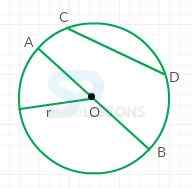
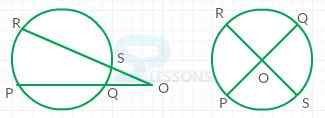
Each and every term of the circle is defined with the help of the below shown figure:
From the figure:
r - radius.
AB - diameter(d).
CD - chord.
O - centre.
- Chord: It is defined as any line segment whose endpoints lie on the circle.
- Sector: It is defined as a region bounded by any two radii and an arc lying between the radii.
- Arc: It is defined as any connected part of the circle.
- Segment: It is defined as a region, bounded by a chord and an arc lying between the chord's endpoints and most importantly not including the center.
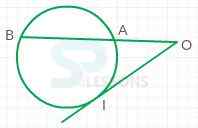
- Secant: It is defined as a straight line that intersects any curve(here circle) in 2 points.
- Tangent: It is defined as a straight line that touches the circle at a single point.
- To any point on the circle itself, the distance from the centre of the circle is known as radius.
- It is represented by the letter 'r'.
- Twice the size of the radius is known as diameter.
- The length of a line segment that passes across a circle through the centre.
- It is indicated by the letter 'd'.
- The circumference of a circle is the distance around the circle, which is analogous to the perimeter of a polygon.
- The ratio of the circumference (C) to the diameter (d) is equal for all the circles and is denoted by the Greek letter 'π' i.e. [latex]\frac{C}{d}[/latex] = π Here, the value of π is approximately equal to 3.14 and can also be approximated by the fraction i.e. [latex]\frac{22}{7}[/latex].
- If the radius of the circle is 'r', then [latex]\frac{C}{d}[/latex] = [latex]\frac{C}{2r}[/latex] = π So, the circumference is related to the radius by the equation i.e. C = 2πr
- A line segment joining any two points on the circumference of a circle is known as chord.
Note:-
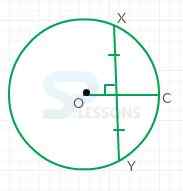
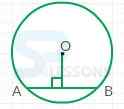
The radius bisects the chord, if a radius of a circle is perpendicular to a chord.
Graphical representation is as shown below:
Here,
OC - radius and XY - chord.
Congruent chords:
- If two chords are the same distance from the centre, in a circle or in congruent circles, then they are congruent.
- Separating the circumference of a circle by any two points into two parts is known as arc.
- Major arc is the bigger curve and minor arc is the smaller curve.
- The arcs that the same degree measure and are in the same circle or in congruent circles is known as congruent arcs.
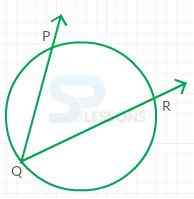
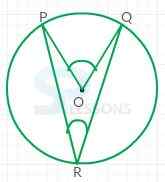
- The angle with its vertex on a circle and with sides that contain chords of the circle is known as inscribed angle.
- When degree measure and measure of radius is known, length of any arc can be found by using the following formula i.e. L = [latex](\frac{n}{360})[/latex]2r Here, L - length, n - degree measure of arc, and r - radius.
- The space its surface occupies is the area of a circle.
- To determine the area of a circle, use the formula i.e. Area = π[latex]r^2[/latex]
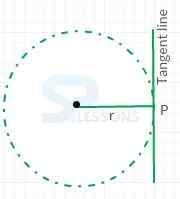
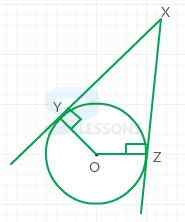
- The line that intersects the circle is known as a tangent, at exactly one point called the point of tangency (P).
- If a line is tangent to a circle, then a radius drawn to the point of tangency is perpendicular to the tangent line.
- Also, if a line is perpendicular to a radius at its end point on the circle, then the line is a tangent to the circle at that end point.
 Samples
Samples
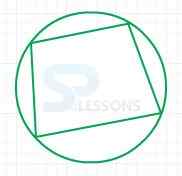
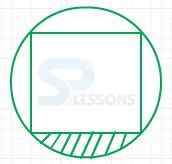
1. In the figure above, if the square inscribed in the circle has an area of 16, what is the area of the shaded region?
Solution:
A. The quantity on the left is greater.
B. The quantity on the right is greater.
C. Both are equal.
D. The relationship cannot be determined without further information.
Solution:
A. The quantity on the left is greater.
B. The quantity on the right is greater.
C. Both are equal.
D. The relationship cannot be determined without further information.
olution:
A. The quantity on the left is greater.
B. The quantity on the right is greater.
C. Both are equal.
D. The relationship cannot be determined without further information.
Solution:
- It is clear from the figure that the area of the shaded region is [latex]\frac{1}{4}[/latex] of the difference between the area of the circle and the area of the square.
Given that,
Area of the square is 16.
So, each side has length 4.
If the radius is known, the area of the circle can be found.
So, draw a diagonal of the square and i.e. the diameter of the circle.
By Pythagorean theorem,
The length of the diagonal = [latex]\sqrt{4^2 + 4^2}[/latex] = 4[latex]\sqrt{2}[/latex].
Then, radius of the circle is r = [latex]\frac{4\sqrt{2}}{2}[/latex] = 2[latex]\sqrt{2}[/latex]
The area of the circle is π[latex]r^2[/latex] = π[latex](2\sqrt{2})^2[/latex] = 8π.
Therefore, area of the shaded region = [latex]\frac{8π - 16}{4}[/latex] = 2π - 4.
- Circle 'A' has radius 'r'.
So, its area is π[latex]r^2[/latex].
Circle B has radius [latex]\frac{3}{4}[/latex]r.
So, its area is π[latex](\frac{3r}{4})^2[/latex] = [latex]\frac{9πr^2}{16}[/latex].
Therefore, the ratio of the area of circle A to the area of circle B is π[latex]r^2[/latex] to [latex]\frac{9πr^2}{16}[/latex], which is the same as the ratio 1 to [latex]\frac{9}{16}[/latex], which is the same as the ratio 16 to 9.
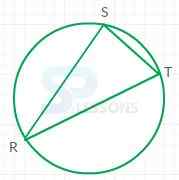
| Quantity A | Quantity B |
| The length of line segment RT | 10 |
- The radius of the circle is 5 and the diameter is 10.
Since the area of the circle is 25π.
Line segment Rt is a diameter of the circle if and only if angle RST is a right angle.
Since, the measure of angle RST is greater than 90 degrees, it follows that the angle RST is not a right angle and the line segment RT is a chord but not a diameter.
Therefore, the length of line segment RT is less than 10.
Hence, option (B) is the right answer.
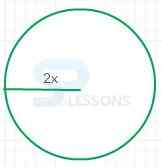
| Quantity A | Quantity B |
| The area of the circle in the figure | The area of the circle with diameter 3y |
- The area of the circle is defined as A = π[latex]r^2[/latex].
The radius of the circle drawn is 2[latex]x[/latex].
So, area = 4[latex]x^2[/latex]π.
The area of the circle with diameter 3[latex]y[/latex] would be a = π[latex]x^2[/latex]
= π[latex](3y)^2[/latex]
= 9π[latex]y^2[/latex]
However, since the values of [latex]x[/latex] and [latex]y[/latex] are not defined, it is impossible to evaluate whether quantity A(4[latex]x^2[/latex][/post_solution_box]π) or quantity B 9π[latex]y^2[/latex] is greater.
Thus, option(D) is right answer.
| Quantity A | Quantity B |
| The length of arc ABC | 1 cm |
- The length of arc ABC can be determined by
Length = [latex]\frac{X}{360}[/latex]C.
Where,
X is the measure of the angle whose rays intersect the arc.
C is the circumference of the circle.
Length = [latex]\frac{X}{360}[/latex]C
= [latex]\frac{36}{360}[/latex] x 10
= [latex]\frac{1}{10}[/latex] x 10
= 1 cm
Therefore, the values in both cases are equal.
Hence, correct option is C.