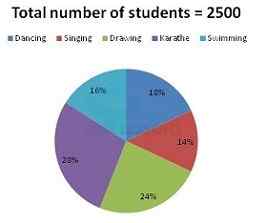
Directions (1 – 5): Study the following information carefully and answer the given questions:
Following pie chart – 1 shows the percentage distribution of total number of students (Boys + Girls) enrolled for different activities in School A and the pie

chart -2 shows the percentage distribution of the total number of girl students enrolled for different activities in School A

1. The total number of boy students enrolled in Dancing and Singing together is approximate what percentage of the total number of girl students enrolled for the same activities?

A. 86 % B. 124 % C. 102 % D. 68 % E. 74 %

Answer: Option C
Explanation: Total number of students enrolled for Dancing = 2500 × ([latex]\frac{18}{100}[/latex]) = 450
Total number of students enrolled for Singing = 2500 × ([latex]\frac{14}{100}[/latex]) = 350
Total number of girl students enrolled for Dancing =1200 × ([latex]\frac{21}{100}[/latex]) = 252
Total number of girl students enrolled for Singing = 1200 × ([latex]\frac{12}{100}[/latex]) = 144
Total number of boy students enrolled for Dancing = 450 – 252 = 198
Total number of boy students enrolled for Singing = 350 – 144 = 206
Required % = [latex]\frac{198 + 206}{252 + 144}[/latex] × 100
= > ([latex]\frac{404}{396}[/latex]) × 100 = 102.02 % = 102 %
2. Find the difference between the total number of students enrolled for Drawing and Karate together to that of total number of girl students enrolled for Karate and Swimming together?

A. 560 B. 700 C. 850 D. 920 E. None of these

Answer: Option B
Explanation: The total number of students enrolled for Drawing and Karathe together
= > 2500 × ([latex]\frac{52}{100}[/latex]) = 1300
The total number of girl students enrolled for Karathe and Swimming together
= > 1200 × ([latex]\frac{50}{100}[/latex]) = 600
Required difference = 1300 – 600 = 700
3. Find the ratio between the total number of boy students enrolled for Dancing and Swimming together to that of total number of girl students enrolled for Drawing and Karate together?

A. 143 : 212 B. 125 : 198 C. 133 : 248 D. 161 : 264 E. None of these

Answer: Option D
Explanation: Total number of students enrolled for Dancing = 2500 × ([latex]\frac{18}{100}[/latex]) = 450
Total number of girl students enrolled for Dancing =1200 × ([latex]\frac{21}{100}[/latex]) = 252
Total number of boy students enrolled for Dancing = 450 – 252 = 198
Total number of students enrolled for Swimming = 2500 × ([latex]\frac{16}{100}[/latex]) = 400
Total number of girl students enrolled for Swimming = 1200 × ([latex]\frac{23}{100}[/latex]) = 276
Total number of boy students enrolled for Swimming = 400 – 276 = 124
The total number of boy students enrolled for Dancing and Swimming together
= > 198 + 124 = 322
The total number of girl students enrolled for Drawing and Karathe together
= > 1200 × ([latex]\frac{44}{100}[/latex]) = 528
Required ratio = 322 : 528 = 161 : 264
4. Find the average number of boy students enrolled for Singing, Drawing, and Karate together?

A. 326 B. 378 C. 412 D. 434 E. None of these

Answer: Option A
Explanation: Total number of students enrolled for Singing = 2500 × ([latex]\frac{14}{100}[/latex]) = 350
Total number of girl students enrolled for Singing= 1200 × ([latex]\frac{12}{100}[/latex]) = 144
Total number of boy students enrolled for Singing = 350 – 144 = 206
Total number of students enrolled for Drawing = 2500 × ([latex]\frac{24}{100}[/latex]) = 600
Total number of girl students enrolled for Drawing = 1200 × ([latex]\frac{17}{100}[/latex]) = 204
Total number of boy students enrolled for Drawing = 600 – 204 = 396
Total number of students enrolled for Karathe = 2500 × ([latex]\frac{28}{100}[/latex]) = 700
Total number of girl students enrolled for Karathe = 1200 × ([latex]\frac{27}{100}[/latex]) = 324
Total number of boy students enrolled for Karathe = 700 – 324 = 376
Total number of boy students enrolled for Singing, Drawing and Karathe together
= > 206 + 396 + 376 = 978
Required average = [latex]\frac{978}{3}[/latex] = 326
5. The total number of students enrolled for Singing and Swimming together is approximately what percentage more/less than the total number of girl students enrolled for Dancing, Drawing and Karate together?

A. 16 % less B. 4 % more C. 4 % less D. 25 % less E. 16 % more

Answer: Option C
Explanation: Total number of students enrolled for Singing and Swimming together
= > 2500 × ([latex]\frac{30}{100}[/latex]) = 750
Total number of girl students enrolled for Dancing, Drawing and Karathe together
= > 1200 × ([latex]\frac{65}{100}[/latex]) = 780
Required % = [latex]\frac{(780 – 750)}{780}[/latex] × 100 = [latex]\frac{30}{780}[/latex] × 100 = 4 % less

Directions (1-5): Study the following information and answer the questions that follow:
There are two companies namely A and B, which sell chairs, tables, and wardrobes in 3 months August, September, and October. The ratio of a chair, tables, and wardrobes sold by A in August are 42: 36: 23 while a ratio of chairs sold by A in August, September, and October is 14: 23: 27. Wardrobes sold by A in August is 230 less than chairs sold in September by A. In September 665 chairs, 400 tables and 210 wardrobes were sold by two companies together. B sold the same number of chairs in Aug and September. The number of tablets sold by company B in September was equal to a number of chairs sold by A in August while the number of wardrobes sold by A in August and B in September was equal. Company B sold a total of 1025 chairs in these three months together which was 480 more than the total number of tables sold by A. Ratio of tables sold by A and B in August is 12: 11 and in October is 35: 38 respectively. The total number of items sold in August was 1075. The total number of wardrobes sold by A in October was 35 less than the wardrobe sold by B in October, while the sum of the wardrobe sold by A and B in October is 205.
1. What is the ratio of the number of tables sold by A in August to that of B in September?

A. 7:6 B. 6:7 C. 12:13 D. 11:12 E. None of these

Answer: Option B
Explanation: Let number of chairs, tables and wardrobes sold by A in August be 42x, 36x and 23x. Also, let chairs sold by A in August, September and October be 14y,
23y and 27y respectively.
∴42x = 14y ⇒y = 3x
and, 23x = 23y – 230
⇒x = 5 and y = 15
Now,
Chairs sold by B in September = 665 – 345 = 320
Chairs sold by B in August = 320
Tables sold by B in September = Chairs sold by A in Aug = 210
∴Table sold by A in September = 400 – 210 = 190
Wardrobes sold by B in September = wardrobes sold by A in Aug = 115
∴Wardrobes sold by A in September = 210 – 115 = 95
Chairs sold by B in October = 1025 – 320 – 320 = 385
Tables sold by A in October = (1025 – 480) – (180 + 190) = 175
Tables sold by B in August = ([latex]\frac{11}{12}[/latex]) × 180 = 165
Tables sold by B in October = ([latex]\frac{38}{35}[/latex]) × 175 = 190
Wardrobes sold by B in August = 1075 – (210 + 320 + 180 + 165 + 115) = 85
Let wardrobes sold by A in October be a and that by B be b in October
∴a = b – 35 and a + b = 205
⇒a = 85 and b = 120

Required Ratio = [latex]\frac{180}{120}[/latex] = [latex]\frac{6}{7}[/latex]
2. Find the number of wardrobes sold by B in October.

A. 80 B. 120 C. 115 D. 95 E. 125

Answer: Option B
Explanation: Refer to the table in Explation of Q1, Wardrobes sold by B in Oct = 120
3. Find the difference in the number of chairs sold by A and B in August.

A. 100 B. 120 C. 105 D. 110 E. 112

Answer: Option D
Explanation: Refer to the table in Explation of Q1, Required difference = 320 – 210 = 110
4. Total number of chairs sold by B in September and October is

A. 750 B. 725 C. 705 D. 715 E. 405

Answer: Option C
Explanation: Refer to the table in Explation of Q1, Total chairs sold by B in September and October = 320 + 385 = 705
5. By what percent tables sold by A in October are more than wardrobes sold by B in October?

A. 83% B. 54% C. 67% D. 56% E. None of these

Answer: Option A
Explanation: Refer to the table in Explation of Q1, [ [latex]\frac{(175-120)}{120}[/latex]] × 100 = 45.83%

Directions (1-5): The Table given below shows the percentage of valid voters in 5 villages in two years 2001 and 2005.
NOTE- Total voters in any year = Valid voters + Invalid voters
1. What is the difference between invalid voters of village C in the two given years if valid voters in 2005 in that village are 4000 and the ratio of valid voters of village C from 2001 to 2005 is 19: 25?

A. 1190 B. 1250 C. 1290 D. 1350 E. 1365

Answer: Option C
Explanation: Invalid voter of village C in 2005 = 4000 × [latex]\frac{36}{64}[/latex] = 2250
Valid voter of village C in 2001 = 4000 × [latex]\frac{19}{25}[/latex] = 3040
Now, invalid voter of village C in 2001 = 3040 × [latex]\frac{24}{76}[/latex] = 960
∴Required diff. = 2250 – 960 = 1290
2. If in village A in 2005, 2500 voters were declared invalid voters 10% of valid voters opted NOTA and the winner got 200 more votes than losing candidate, then find the total vote that losing candidate got in 2005 in village A.

A. 4400 B. 4600 C. 5400 D. 5200 E. 4800

Answer: Option A
Explanation: Total valid votes of village A in 2005 = 2500 × [latex]\frac{100}{20}[/latex] × [latex]\frac{80}{100}[/latex] = 10000
Total valid votes excluding Nota in village A in 2005 = 10000 × [latex]\frac{90}{100}[/latex] = 9000
∴According to question,
x + (x + 200) = 9000
⇒ x = 4400
Required no. of votes of losing candidates = 4400
3. In village B if the ratio of total voters in 2001 to 2005 is 26: 23, then find the ratio of invalid voters in 2001 to the invalid voters in 2005 in same village.

A. 131: 160 B. 130: 161 C. 127: 141 D. 18: 35 E. None of these

Answer: Option B
Explanation: Let the total voters in 2005 are x.
Total voters in 2001 = ([latex]\frac{26}{23}[/latex]) x
∴ [latex]\frac{\frac {75}{100} × \frac{30}{100} × x }{\frac{30}{100} × x }[/latex] = [latex]\frac{130}{161}[/latex]
4. If there are 1600 males invalid voters of village E in 2001 and the females' invalid voters of the same village and same year contributed is 36% of total valid voters, then find the percentage of invalid male voters in a total population if total males in village E in 2001 were 2000.

A. 2% B. 4% C. 6% D. 8% E. 8%

Answer: Option D
Explanation: Total invalid male of village E in 2001
= 2000 – 1600 = 400
Total valid voters in 2001 = 1600 × [latex]\frac{100}{64}[/latex] = 2500
Total Voters in 2001 = 2500 × [latex]\frac{100}{80}[/latex] = 3125
∴ required % = ([latex]\frac{400}{3125}[/latex]) × 100 = 12.8 %
5. If the ratio of valid voters of village B in 2001 and invalid voters of village D in 2005 was 16: 3, then total voters of village D in 2005 were what percent more or less than those of village B in 2001?

A. 45 [latex]\frac{2}{7}[/latex] % B. 53 [latex]\frac{4}{5}[/latex] % C. 53 [latex]\frac{1}{8}[/latex] % D. 52 [latex]\frac{1}{8}[/latex] % E. 50 [latex]\frac{2}{5}[/latex] %

Answer: Option C
Explanation: Let total voters of village B in 2001 = x
& Total voters of village D in 2005 = y [latex]\frac{\frac{20x}{3}}{80}[/latex]
∴ [ [latex]\frac{\frac {75}{100} × x}{\frac{30}{100} × y}[/latex] ] = [latex]\frac{16}{3}[/latex]
[latex]\frac{x}{y}[/latex] = [latex]\frac{32}{15}[/latex]
Required % = [latex]\frac{17}{32}[/latex] × 100 = 53 [latex]\frac{1}{8}[/latex] %