Introduction
Introduction
Line Graphs are represented by specific points joined together by straight lines. The points are plotted on a two-dimensional plane taking one parameter on the horizontal axis and the other on vertical axis.
Quantitative Aptitude -BANKING|SSC|RAILWAYS|INSURANCE|RECRUITMENT EXAMS - EBOOKS
 Methods
Methods
Line graphs are categorised into two types. They are:
1. One dependent variable historigram,
2. Multi dependent variable historigram.
- Historigram is a graph of time series where the changes in a given variable is illustrated s a function of time.
- From one period of time to another, the graph shows changes in the value of one or more variables.
- These graphs can be either on a natural scale or on a ratio scale.
- Natural scale is used, if the absolute values of a variable are to be represented. In natural scale, equal distances on an axis represent equal values/amounts.
- One dependent variable historigram is the simplest type. The values of only one variable is to be plotted along the Y-axis and as the time factor being independent variable, it is taken on X-axis.
- In more than one dependent variable historigram, distribution of two variables is represented distinctly. For all values, the vertical scale is common.
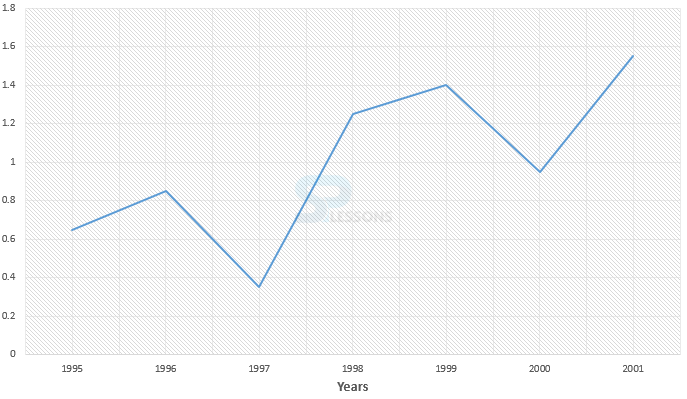
- A. 87.5%
B. 37.5%
C. 9.09%
D. None of these
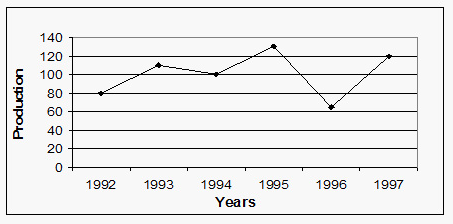
- Here we look up the values of the production for the 2 years first. Locate 1993 on the X axis, which denotes years. Move vertically up along the Y axis direction in 1993, and we get value of production in 1993 as 110. In the same way we get the value of production in 1994 as 100.
In calculating % increases & decreases: In this case 1993, it is very important to remember that the original year is the one that is used as the reference year.
Which is 110 – 100 = 10.
Now we have to express 10 as a percentage of the production in 1993, which is 110.
So the required answer is 100 × 10/110 = 9.09%. Hence answer is option C.
- A. 1996
B. 1992
C.1995
D. 1994
- The production in 1994 was 100, that in 1996 was 62.5.
The average production of 1994 and 1996 = (100 + 62.5)/2 = 81.25.
This was approximately equal to production in 1992. Hence Answer is option B.
- A. 1
B. 2
C. 3
D. 4
- Average production for 6 years = 80 + 110 + 130 + 100 +120 +65 / 6 = 101
Clearly in 1992, 1994 and 1996, the production was less than average. Hence answer is option C.
- A. 120 units
B. 100 units
C.60 units
D. 50 units
- The production in 1992 is 80 units. The Required production in 1991 =
80 / 160 x 100 = 50 Hence answer is option D.
- A. 1997
B. 1996
C.1995
D. 1994
- Here remember that absolute increase has been asked. The difference in Y coordinates of the adjacent years will give us the increase. Since the distance between consecutive years is the same on the X axis, we can check the slopes of various segments. By visual inspection, maximum increase in food grain production has been in the year 1997 (55 units by calculation).Hence, answer is option A
- A. 700
B. 800
C. 650
D. 193.03
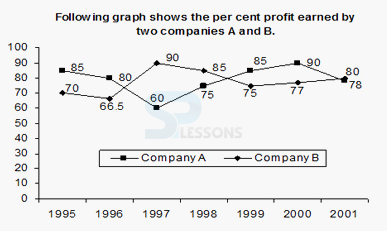
- Investment of company A in 2000 = 1239 x 100 / 177 = Rs.700 lakh
- A. 10%
B. 102(2/3) %
C. 106(2/3) %
D. None of these
- Let us assume the investment of Company B in 1997 is Rs. 100. Investment of company B in 1998 was 20% more than that in the previous year.
So the investment of Company B in 1998 is Rs. 120.
Profit in 1997 of company B= 90 % of 100 = Rs. 90
Profit in 1998 of company B= 85% of 120 = Rs. 102.
Required % = 102 / 90 x 100 = 113 (1/3) %
- A. 2001
B. 1995
C. 1998
D. 2000
- Quicker Method: The ratio of investment and profit will be maximum when percentage profit is minimum. Therefore, the ratio of investment and profit will be maximum in 2001.
- A. 9 : 10
B. 10 : 9
C. 13 : 15
D. 15 : 13
- Required ratio = (100 / 185) x (166.5 / 100) = (333 / 370) = (37*9 / 37*10) = 9:10
- A. 1995
B. 1999
C. 2000
D. Can't be determined
- We don’t have the data for investment. So, we can't determine the answer.
 Samples
Samples
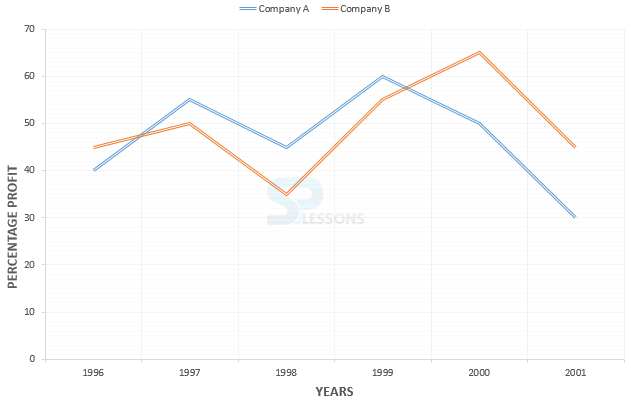
1. Study the following graph carefully and answer the given questions:
%profit = [latex]\frac{Income - Expenditure}{Expenditure}[/latex] x 100
1. If the income of company A in 1998 was equal to its expenditure in 2000, what was the ratio between company's expenditure in the years 1998 and 2000 respectively?
1. Required percentage = [latex]\frac{3000}{3200} * 100[/latex]% = 93.75%
So, option (B) is correct answer.
2. From the given data, the number of students studying in the school during 1999 = 3150.
So, option (D) is correct answer.
3. Required percentage = [latex]\frac{300}{450} * 100[/latex]% = [latex]\frac{2}{3}[/latex]
So, option (D) is correct answer.
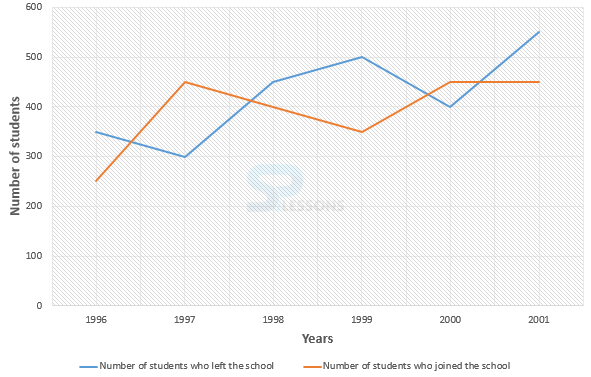
4. The percentage rise/fall in the number of students who left the school (compared to the previous year) during various years are:
For 1997 = [latex]\frac{450 - 250}{250} * 100[/latex]% = 80% (rise)
For 1998 = [latex]\frac{450 - 400}{450} * 100[/latex]% = 11.11% (fall)
For 1999 = [latex]\frac{400 - 350}{400} * 100[/latex]% = 12.5% (fall)
For 2000 = [latex]\frac{450 - 350}{350} * 100[/latex]% = 28.57% (rise)
For 2001 = [latex]\frac{450 - 450}{450} * 100[/latex]% = 0% (rise)
Hence, in the year 1997 maximum rise/fall occured.
So, option (A) is correct answer.
- (A) 29 : 20
(B) 20 : 29
(C) 19 : 20
(D) cannot be determined
(E) None of these.
- (A) 8
(B) 10
(C) 10.4
(D) All of these
(E) None of these.
- 1. Since the data given is inadequate hence it cannot be determined.
So, the option(D) is correct answer.
2. The expenditure of company B in 2001 = [latex]\frac{5}{9} * 18[/latex] = 10 lakhs
Let the income of company B be Rs.[latex]x[/latex] lakh
Therefore, 40 =[latex]\frac{x - 10}{10} * 100[/latex]
40 = 10[latex]x[/latex] - 100
10[latex]x[/latex] = 140
[latex]x[/latex] = 14 lakh.
- (A) 50000
(B) 42000
(C) 33000
(D) 21000
(E) 13000
- (A) 19000
(B) 22000
(C) 26000
(D) 28000
(E) 29000
- (A) 173
(B) 164
(C) 132
(D) 97
(E) 61
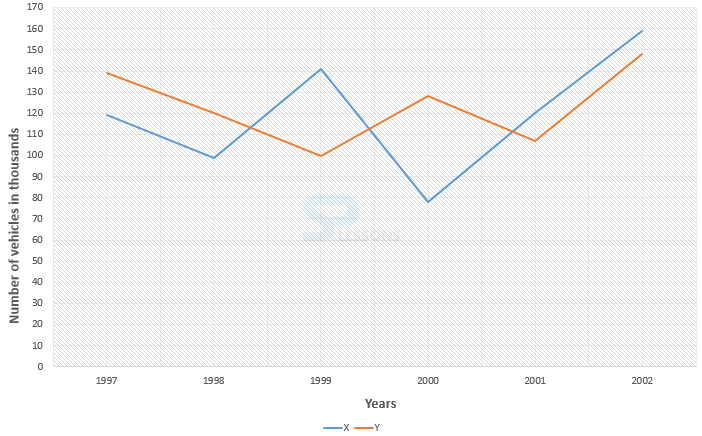
- 1. Required difference = 128000 - 107000 = 21000.
So, option (D) is correct one.
2. Total production of company X from 1997 to 2002 = 119000 + 99000 + 141000 + 78000 + 120000 + 159000 = 716000.
Total production of company Y from 1997 to 2002 = 139000 + 120000 + 100000 + 128000 + 107000 + 148000 = 742000.
Difference = 742000 - 716000 = 26000.
So, option (C) is correct answer.
3. Required percentage = [latex]\frac{128000}{78000} * 100[/latex]% = 164%
So, option (B) is correct answer.
1. Ratio of imports to exports in the year 1996 = 0.85.
Let the exports in 1996 = Rs. [latex]x[/latex] crores.
Then,
[latex]\frac{272}{x}[/latex] = 0.85
⇒ [latex]x[/latex] = [latex]\frac{272}{0.85}[/latex] = 320
Therefore, exports in 1996 = Rs. 320 crores.
So, option (B) is correct answer.
2. The exports are more than the imports implies that the ratio of value of imports to exports is less than 1.
Now, this ratio is less than 1 in the years 1995, 1996, 1997, and 2000.
Thus there are four such years.
So, option (D) is correct answer.
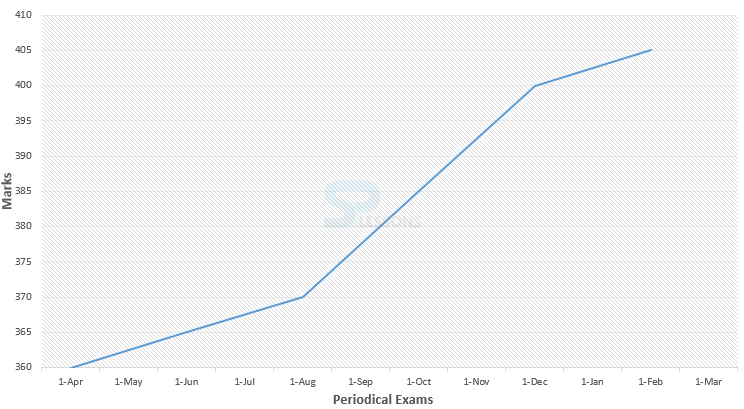
Model 4: Periodical examinations are held every second month in a school. In a session during April 2001 to March 2002, a student of class IX appeared for each of the periodical exams. The aggregate marks obtained in each periodical exam are represented in the below given line graph. Study it and answer the given questions.
1. What is the percentage of marks obtained by the student in the periodical exams of August 01 and October 01 taken together?
(A) 73.25%
(B) 75.5%
(C) 77%
(D) 78.75%
(E) 79.5%
2.The total number of marks obtained in February 02 is what percent of the total marks obtained in April 01?
(A) 110%
(B) 112.5%
(C) 115%
(D) 116.5%
(E) 117.5%
Solution:
1. Required percentage = [latex]\frac{370 + 385}{500 + 500} * 100[/latex]% = [latex]\frac{755}{1000} * 100[/latex]% = 75.5%
So, option (B) is correct answer.
2. Required percentage = [latex]\frac{405}{360} * 100[/latex]% = 112.5%
So, option (B) is correct answer.
Model 5: Study the following line graph which gives the number of students who joined and left the school in the beginning of year for six years, from 1996 to 2001.
Initial strength of school in 1995 = 3000
1. The number of students studying in the school in 1998 was what percent of the number of students studying in the school in 2001?
(A) 92.13%
(B) 93.75%
(C) 96.88%
(D) 97.25%
2. What was the number of students studying in the school during 1999 ?
(A) 2950
(B) 3000
(C) 3100
(D) 3150
3. The ratio of the least number of students who joined the school to the maximum number of students who left the school in any of the years during the given period is?
(A) 7:9
(B) 4:5
(C) 3:4
(D) 2:3
4.For which year, the percentage rise/fall in the number of students who left the school compared to the previous year is maximum?
(A) 1997
(B) 1998
(C) 1999
(D) 2000
Solution: