Introduction
The triangle is a convex polygon with three line portions joining three non-collinear points.
As shown above in the figure, each of the three line segments is known as a side and each of three non-collinear points is known as a vertex.
Quantitative Aptitude -BANKING|SSC|RAILWAYS|INSURANCE|RECRUITMENT EXAMS – EBOOKS
Methods
Triangles can be categorized by the number of equal (or congruent) sides they have.
Let the lengths of the sides be \(a\) and \(b\).
The hypotenuse has length \(c\).
Using the Pythagorean theorem,
\(a^2\) + \(b^2\) = \(c^2\).
Solution:
Solution:
- A triangle with no equal sides is a scalene triangle,
- A triangle with two equal sides is an isosceles triangle, and
- A triangle with three equal sides is an equilateral triangle.
Triangle inequality rule: The length of any side of a triangle will always be less than the sum of the lengths of the other two sides and greater than the difference of the lengths of the other two sides.
Sum of the interior angles: The sum of the angles of a triangle is 180 degrees.
Sum of the exterior angles: The sum of the angles of a triangle is 360 degrees.
Types of triangles:
Equilateral triangle:
- All the three sides of equal length.
- Each angle in an equilateral triangle is equal to 60 degrees.
Isosceles triangle: A triangle having two of its sides of equal length is known as isosceles triangle.
Scalene triangle: A triangle having three sides of different lengths is known as scalene triangle.
Acute triangle: A triangle having three acute angles is known as acute triangle. That is, if all three angles of a triangle are less than 90°, then it is an acute triangle.
Obtuse triangle:-
- A triangle having an obtuse angle is known as obtuse triangle.
- One of the angles of the triangle measures more than 90 degrees.
Right Angled triangle:-
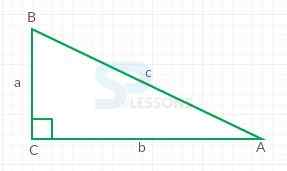
- A triangle having a right angle is known as right angle triangle.
- Side opposite to the right angle is known as hypotenuse.
- The two sides that form the right angle are called the legs.
Pythagorean theorem:-
In a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
This is known as Pythagorean theorem.
Consider the below given right angle triangle,
The hypotenuse has length \(c\).
Using the Pythagorean theorem,
\(a^2\) + \(b^2\) = \(c^2\).
Area of a triangle:
Consider a triangle with base of length \(b\) and height \(h\) as shown below.
The area of the triangle = \(\frac{1}{2}\) x \(b\) x \(h\).
Properties of triangles:
- An angle, lying opposite the greatest side, is also the greatest angle and vice versa.
- Angles, lying opposite the equal sides, are also equal and vice versa.
Theorems about congruency of triangles:
Two triangles are congruent, if they have accordingly equal:
i) Two sides and an angle between them,
ii) Two angles and a side, adjacent to them,
iii) all the three sides are equal.
Theorems about congruency of right-angled triangles:
Two right-angled triangles are congruent, if one of the following conditions is valid:
i) Their sides are equal,
ii) A side and a hypotenuse of one of triangle are equal to a leg and a hypotenuse of another.
ii) A hypotenuse and an acute angle of one of triangles are equal to a hypotenuse and acute angle of another.
Orthocenter:
Three heights (altitude) of triangle always intersect in one point, called an orthocenter of a triangle.
Altitude: It is a perpendicular, dropped from any vertex to an opposite side. this side is called a base of triangle.
Note:-
1. An orthocenter of an acute-angled triangle is placed inside of the triangle.
2. An orthocenter of an obtuse-angled triangle outside of the triangle.
3. An orthocenter of a right-angled triangle coincides with a vertex of the right angle.
1. An orthocenter of an acute-angled triangle is placed inside of the triangle.
2. An orthocenter of an obtuse-angled triangle outside of the triangle.
3. An orthocenter of a right-angled triangle coincides with a vertex of the right angle.
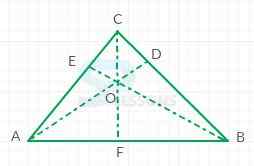
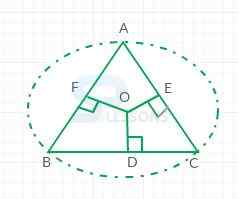
Centroid:
Intersecting point of median is known as centroid as shown in the figure below. This point divides each median by ratio 2:1, considering from a vertex.
Median:
Median is a line segment, joining any vertex of triangle and a midpoint of the opposite side.
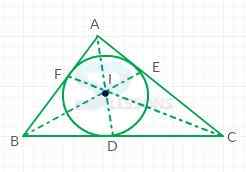
In-center:
Intersecting point of angle bisector is known as in-center.
Angle bisector:
It is a line segement from a vertex to a point of intersection with an opposite side.
Note:-
Angle of bisector divides an opposite side into two parts, proportional to the adjacent sides.
Angle of bisector divides an opposite side into two parts, proportional to the adjacent sides.
Circumcenter:
- Intersecting point of mid-perpendicular bisector of side is known as circumcenter.
- Mid-perpendicular is a perpendicular drawn from a middle point of a side.
Note:-
1. In an acute angled triangle circumcenter lies inside of the triangle.
2. In an obtuse angled triangle circumcenter lies outside of the triangle.
3. In a right angled triangle circumcenter lies in the middle of the hypotenuse.
4. An orthocenter, a centroid, an in-center and a circumcenter coincide only in an equilateral triangle.
1. In an acute angled triangle circumcenter lies inside of the triangle.
2. In an obtuse angled triangle circumcenter lies outside of the triangle.
3. In a right angled triangle circumcenter lies in the middle of the hypotenuse.
4. An orthocenter, a centroid, an in-center and a circumcenter coincide only in an equilateral triangle.
Example 1:
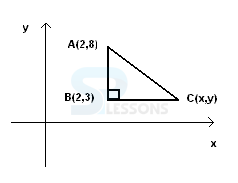
The right triangle shown below has an area of 25. Find its hypotenuse.
- Since the x coordinates of points A and B are equal, segment AB is parallel to the y axis. Since BC is perpendicular to AB then BC is parallel to the x axis and therefore y, the y coordinate of point C is equal to 3.
We now need to find the x coordinate x of point C using the area as follows.
Area = 25 = (1/2) d (A, B) * d (B, C)
d (A, B) = 5
d (B, C) = |x – 2|
We now substitute d(A,B) and d(B,C) in the area formula above to obtain.
25 = (1/2) (5) |x – 2|
We solve the above as follows
|x – 2| = 10
x = 12 and x = – 8
We select x = 12 since point C is to the left of point B and therefore its x coordinate is greater than 2.
We have the coordinates of point A and C and we can find the hypotenuse using the distance formula.
hypotenuse = d(A,C) = sqrt[\( (12 – 2)^{2}\) + \((3 – 8)^{2}\)]
= sqrt(125) = 5 sqrt(5)
Example 2:
Triangle ABC shown below is inscribed inside a square of side 20 cm. Find the area of the triangle
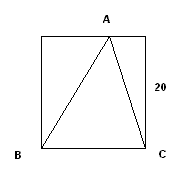
- The area is given by
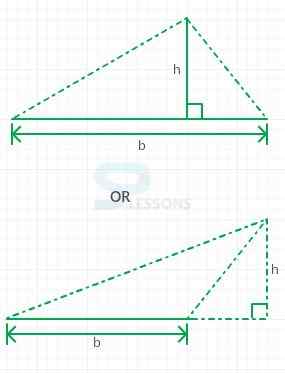
Area of triangle = (1/2) base * height
= (1/2)(20)(20) = \(200 cm^{2}\)
Samples
1. What is the area of isosceles right angled triangle if its legs are 5 and 24 units?
Solution:
Solution:
Solution:
- Given
Legs of a isosceles right angled triangle. So,
Let
Breadth be \(b\) = 5 units.
Height be \(h\) = 24 units.
Area of the triangle = \(\frac{1}{2}\) x \(b\) x \(h\)
= \(\frac{1}{2}\) x 5 x 24 = 60 units.
2. If AB = BD, BC = CD and \(\angle\)ACD = \({80}^{\circ}\), what is the measure in degrees of \(\angle\)BAD?
Solution:
- Given that,
AB = BD
BC = CD
\(\angle\)ACD = \({80}^{\circ}\)
Since AB = BD,
\(\angle\)CBD = \(\angle\)CDB.
There is \({100}^{\circ}\) left in the triangle.
So, each of these angles is \({50}^{\circ}\).
\(\angle\)DBA is supplementary to \(\angle\)DBC making it \({130}^{\circ}\).
Since BA = BD,
\(\angle\)BAD = \(\angle\)BDA.
There is \({50}^{\circ}\) left in the triangle. So, each of these angles is \({25}^{\circ}\).
3. In the figure given, DE\(\parallel\) BC. Find the length of DE?
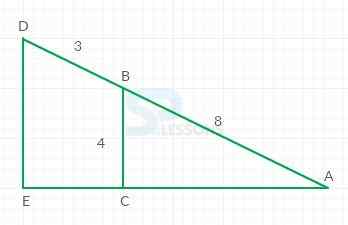
- Given that,
DE\(\parallel\) BC
So, \(\bigtriangleup\)ADE ≅ \(\bigtriangleup\)ABC.
Now, \(\frac{4}{DE}\) = \(\frac{6}{9}\)
DE = 6 inches.
4.
| Quantity A | Quantity B |
| Area of \(\bigtriangleup\)Q | 8 sq. m. |
A. The quantity on the left is greater.
B. The quantity on the right is greater.
C. Both are equal.
D. The relationship cannot be determined without further information.
Solution:
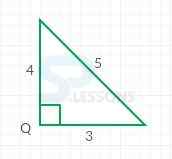
- Given that
Q is a right angled triangle.
Area of the triangle = \(\frac{1}{2}\) x \(b\) x \(h\)
Let, 3 and 4 be \(b\) and \(h\).
So, A = \(\frac{1}{2}\) x 3 x 4
A = 6.
Therefore, area of \(\bigtriangleup\)Q is 6 sq.m. which is less than 8 sq.m.
Hence, correct option is B.
5.
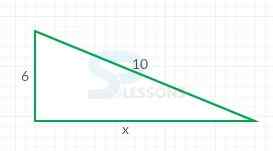
| Quantity A | Quantity B |
| 9 | \(x\) |
A. The quantity on the left is greater.
B. The quantity on the right is greater.
C. Both are equal.
D. The relationship cannot be determined without further information.
Solution:
- By using Pythagorean theorem,
\(a^2\) + \(b^2\) = \(c^2\)
⇒ \(6^2\) + \(x^2\) = \(10^2\)
⇒ 36 + \(x^2\) = 100
⇒ \(x^2\) = 64
⇒ \(x\) = 8
Therefore, 8 is less than 9.
Hence, option A is correct.